Методические указания к лабораторным работам "Изучение законов сохранения при соударении двух шаров", "Изучение вращательного движения на маховике Обербека", "Изучение закона сохранения момента импульса", "Измерение момента инерции маятника Максвелла", страница 12

Пример расчёта момента импульса L_iдо разлёта грузов:

L_i = [I₁+I₂+I_П]w_1i.

Пример расчёта момента импульса L_i¢системыпосле разлёта грузов:

L_i¢= [I₁¢+I₂¢+I_П]w_2i.

Сопоставьте значения моментов импульса до и после разлета грузов и проанализируйте причины, которые приводят к некоторым отличиям в полученных результатах.

ВНИМАНИЕ:

1. Включать в сеть измерительный блок L-микро можно только послеего подключения к разъему последовательного порта компьютера.

2. Перед раскруткой системы убедитесь в правильной установке ограничителей хода грузов.

Контрольные вопросы

1. Что называется моментом импульса тела относительно некоторой точки? Как выглядит соответствующая формула в случае абсолютно твёрдого тела?

2. Сформулируйте закон сохранения момента импульса. Приведите пример проявления этого закона на практике.

3. Сформулируйте теорему Штейнера и приведите примеры её применения для расчётов в настоящей лабораторной работе.

43

4. Выведите формулу (13 ) момента импульса подвижной части системы.

5. Проанализировав результаты проведённых измерений, объясните, что является основным источником погрешностей в определении момента импульса системы.

РЕКОМЕНДУЕМАЯ  ЛИТЕРАТУРА

1. Савельев И. В. Курс общей физики: В 3-х т. – М.: Наука, 1987. – Т. 1, 432 с.

2. Яворский Б.М., Детлаф А.А. Курс физики. – М.: Высш. шк., 2000.

3. Расчет погрешностей в лабораторных работах физического практикума. Методические указания к вводным занятиям в физическом практикуме/ Н.А. Гринчар, Ф.П. Денисов, Б.А. Курбатов и др.; Под общ. ред. Ф.П. Денисова. - М.: МИИТ, 1995. - 38 с.

44

 

РАБОТА  № 6-П

ИЗМЕРЕНИЕ МОМЕНТА ИНЕРЦИИ МАЯТНИКА МАКСВЕЛЛА

Цель работы. Определение момента инерции симметричного твердого тела (диска).

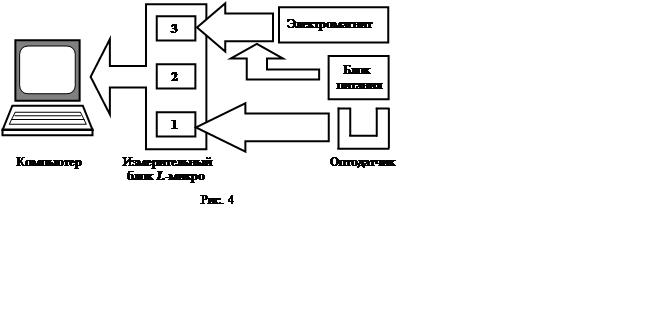
Приборы и принадлежности:  Штатив универсальный, маятник Максвелла, электромагнит, оптодатчик, измерительный блок L-микро, блок питания, линейка.

Введение

Момент инерции тела Iотносительно некоторой оси является мерой инертности тела при вращении его вокруг этой оси. Для материальной точки момент инерции равен произведению ее массы на квадрат расстояния до оси вращения:

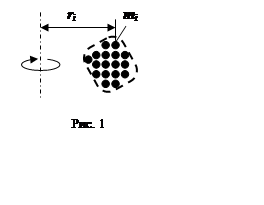I = mr²,

а для тела, которое можно представить в виде системы боль­шого количества материальных точек (рис. 1.), момент инерции относительно некоторой оси вращения равен сумме произведений масс всех материальных точек на квадраты их расстояний до этой оси:

I=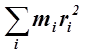

Конструирование технических устройств, содержащих вращающиеся детали (на железнодорожном транспорте, в самолетостроении, электротехнике и т.д.), требует знания величин моментов инерции этих деталей. При сложной форме тела теоретический расчет его момента инерции может оказаться трудно выполнимым. В этих случаях предпочитают измерить момент инерции нестандартной детали опытным путем.

45

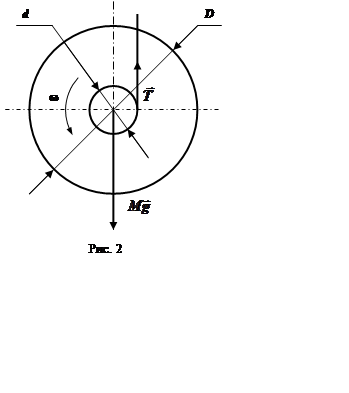В работе определяется момент инерции маятника Максвелла – диска, неподвижно установленного на горизонтальной оси. На концах оси симметрично относительно диска закрепляются нити, с помощью которых маятник подвешивается к штативу. При вращении оси нити могут наматываться на ось или разматываться, обеспечивая тем самым перемещение маятника вверх и вниз. Если, намотав нити на ось, поднять маятник на некоторую высоту и отпустить его, то он начнет совершать колебательное движение в поле силы тяжести. В нижней точке маятник приобретает наибольшую скорость вращения, и, продолжая вращаться по инерции, снова поднимается на некоторую высоту за счет наматывания нитей на ось. После достижения верхней точки, где скорость вращения маятника становится равной нулю, он начинает падать, вращаясь при этом в другую сторону.

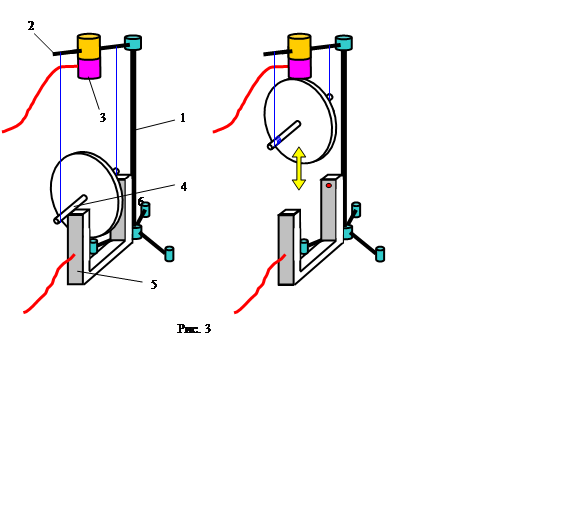На рис. 2 показана схема сил, действующих на вал маятника. Движение маятника осуществляется под действием силы тяжести  и силы натяжения нитей .

Движение маятника вниз является равноускоренным до тех пор, пока нити хотя бы частично намотаны на вал. При этом угловая скорость w вращения диска вокруг оси симметрии и линейная скорость u самой оси диска связаны между собой соотношением:

u=w ,                                             (1)

где d - диаметр вала, на который намотана нить. (Иными словами, скорость движения центра масс маятника равна скорости сматывания нитей с вала).

Кинетическая энергия диска складывается из кинетической энергии вращательного движения диска относительно оси симметрии и кинетической энергии его поступательного движения:

I= ,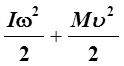

где I -момент инерции маятника, М – его масса.

С учётом формулы (1)

46

47

                                               

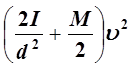I= .                                              (2)

Согласно закону сохранения энергии в изолированной системе, в которой действуют лишь консервативные* силы, полная механическая энергия системы остаётся постоянной величиной.

В соответствии с этим законом при движении в поле силы тяжести кинетическая энергия маятника, который опустился с высоты h, равна его потенциальной энергии на этой высоте:

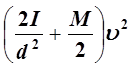 =Мgh.                                 (3)

Движение маятника – равнопеременное, с постоянным ускорением. В этом случае скорость u выражается через высоту падения h и время движения t на основании кинематических соотношений:

u=at ,                                               (4)

h= ,                                             (5)

где а - ускорение, с которым движется центр масс диска. Из формул (4), (5) следует

u  = .                                              (6)

Подставив выражение (6) в уравнение (3) и решив его относительно I, получим расчетную формулу для экспериментального определения момента инерции I_Э маятника Максвелла относительно его оси симметрии

I_Э= 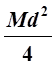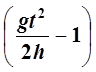.                                           (7)