Из приведённых выше формул следует, в частности, что аналогом массы при вращательном движении является момент инерции I; определению Iмаховика Обербека при различных положениях грузов на спицах и посвящена настоящая работа.
Напомним, что момент инерции тела Iотносительно некоторой оси является мерой инертности тела при вращении его вокруг этой оси. Для материальной точки момент инерции равен произведению ее массы на квадрат расстояния до оси вращения:
I = mr2,
а для тела, которое можно представить в виде системы большого количества материальных точек (рис. 1.а), момент инерции относительно некоторой оси вращения равен сумме произведений масс всех материальных точек на квадраты их расстояний до этой оси:
|
.
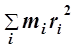(1)
 |
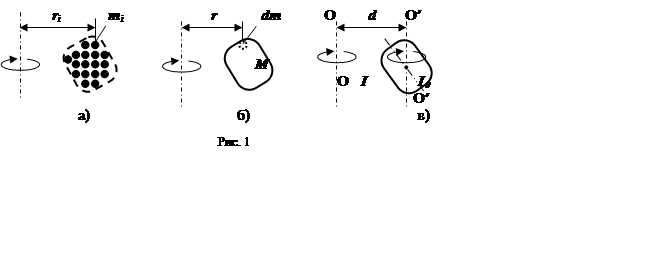Для вычисления момента инерции сплошного тела его мысленно разбивают на бесконечное малые области с массами dm, каждая из которых находится на своём расстоянии r от оси вращения (рис. 1.б); I находят интегрированием по всем этим областям:
I=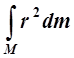
.
Понятно, что момент инерции зависит не только от общей массы тела, но и от формы тела, а также – от распределения массы по его объёму (так, например, какие-то части тела могут быть изготовлены из более тяжёлого материала, а какие-то – из более лёгкого).
Ось вращения может проходить через центр масс тела, а может и находиться вне его (рис. 1.в). Во втором случае для вычисления момента инерции пользуются теоремой Штейнера.
Момент инерции тела I относительно произвольной оси равен сумме момента инерции I0 относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела т на квадрат расстояния d между осями:
I = I0 + md2. (2)
При конструировании технических устройств, содержащих вращающиеся детали (на железнодорожном транспорте, в самолетостроении, электротехнике и т.д.), требуется знание величин моментов инерции этих деталей. При сложной форме тела теоретический расчет его момента инерции может оказаться трудно выполнимым. В этих случаях предпочитают измерить момент инерции нестандартной детали опытным путем.
|
При выполнении
лабораторной работы Вам необходимо измерить момент инерции маятника Обербека в
двух случаях: в отсутствие грузов на стержнях и при максимальном удалении
грузов от оси вращения. В каждом случае раскрутка маятника проводится одним из
двух перегрузков (6) – по выбору преподавателя.
Рассмотрим движение маятника Обербека, используя законы динамики. Перегрузок (6) массой тП на нити (5) движется поступательно с ускорением a под действием силы тяжести mПg и силы натяжения нитиT. Можно записать уравнение второго закона Ньютона для этого груза:
mПg - T = mПa. (3)
Отсюда находим силу натяжения нити: Т = тП(g - а) и вычисляем момент M этой силы относительно оси вращения:
M = Tr = тП(g - а)r , (4)
где r – радиус цилиндрической поверхности-муфты, на которую намотана нить).
|
тП(g - а)r = I·e, (5)
где e - угловое ускорение вращающегося маятника, причём а = er.
Эта формула может быть использована для определения момента инерции I1 крестовины с грузами:
I1= mП(g -e1r)r/e1 (6)
и без грузов:
I2= mП(g -e2r)r/e2. (7)
Момент инерции крестовины с грузами может быть также представлен в виде:
I1= I2 + Iг , (8)
где Iг – момент инерции четырёх грузов.
Таким образом, появляется возможность экспериментального определения момента инерции грузов на крестовине:
Iг = I1- I2 = mП(g -e1r)r/e1- mП(g -e2r)r/e2. (9)
Результаты вычислений по формуле (9) предлагается сравнить с теоретическим значением момента инерции грузовIг*, рассчитываемым в предположении, что размерами грузов много меньше расстояния от их центра до оси вращения крестовины:
Iг* = m1R1 2+ m2R2 2 + m3R3 2 + m4R4 2, (10)
в которой m1,m2 ,m3 иm4 – массы каждого из четырёх грузов, а R1,R2 , R3 и R4 – расстояния от центров этих грузов до оси вращения.
Порядок выполнения работы
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.