Методические указания к лабораторным работам "Изучение законов сохранения при соударении двух шаров", "Изучение вращательного движения на маховике Обербека", "Изучение закона сохранения момента импульса", "Измерение момента инерции маятника Максвелла", страница 17

Согласно закону сохранения импульса суммарный импульс замкнутой системы не меняется со временем, следовательно, можно записать:

mu=(М + т)и.                                          (1)

Здесь mu– импульс пульки до удара, (М + т)и – импульс маятника с застрявшей в цилиндре после удара пулькой, (m– масса пульки, М – масса баллистического маятника). Масса спицы мала по сравнению с массой цилиндра, ей можно пренебречь. Из равенства (1) определим скорость маятника в момент времени непосредственно после завершения процесса столкновения:

и = 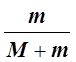u.                                            (2)

Интервал времени столкновения    Dt₁ во много раз меньше времени Dt₂ = t₃ - t₂ подъёма ма­ятника (Dt₁<<Dt₂), поэтому за время столкновения шарик уже практически остановится относительно цилиндра, сообщив последнему начальную скорость, а цилиндр еще не успеет сдвинуться на заметную величину. Таким образом, две части процесса превращения энергии происходят последовательно друг за другом, и рассматривать их можно раздельно.

Рассмотрим теперь систему пулька – цилиндр – земля. Эта система замкнута и, кроме того, во время подъёма в ней действуют уже только консервативные силы (трением в подшипнике на оси датчика поворота пренебрегаем). Вспомним закон сохранения механической энергии: в замкнутой системе, в которой действуют лишь консервативные силы, полная механическая энергия не меняется со временем.

Сказанное означает, что кине­тическая энергия, которую приобретает маятник к моменту времени t₃перейдет в потенциальную энергию поднятой на высоту h массы (М + т) цилиндра с пулькой внутри.

Кинетическая энергия W_К в начале движения системы записывается так:

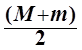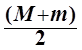
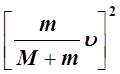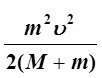W_К  = u²= = .            (3)

Потенциальная энергия W_П поднятого на высоту h маятника равна:

64

W_П=(М + т)gh ,                                        (4)

и на основе закона сохранения энергии можно записать:

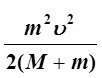= (М + т)gh.                                  (5)

Решая уравнение (5) относительноu, получаем:

u=.                                       (6)

Высота поднятия центра масс маятника при известном расстоянии l от точки подвеса до цилиндра определяется по углу отклонения a маятника, который измеряется датчиком угла поворота.

На рис. 2в схематически показано как происходит поднятие маятника на высоту h в результатеего отклонения на уголa. Из прямоугольного треугольника ОА'С следует, что

ОС = Н = l соs a,

h=АО - ОС = l - Н = l -  l cos a, или:

h = l (1 -соs a)                                         (7)

 Подставляя (7) в (6), получим расчетную формулу для определения скорости шарика:

u=, или

u= 2sin.                                  (8)

Порядок выполнения работы

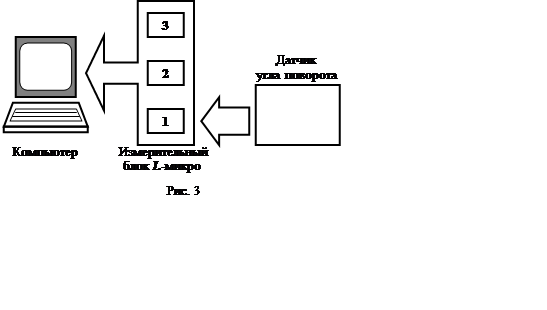
1. Соберите установку как показано на рис. 1. Обратите внимание на то, что ось вращения датчика должна быть горизонтальной, а ось цилиндра должна располагаться в плоскости колебаний маятника.

С помощью линейки измерьте расстояние от оси цилиндра баллистического маятника до оси вращения датчика угла поворота. Полученную величину запишите в таблицу 1. Туда же занесите значения массы цилиндра маятника и пульки (указаны на установке).

65

2. Подключите измерительный блок L-микро к разъему последовательного порта компьютера. После этого подсоедините его к сети (220 В, 50 Гц) и включите. Разъем датчика угла поворота присоедините к первому каналу измерительного блока (рис. 3). Включать в сеть измерительный блок L-микро можно только после его подключения к разъему последовательного порта компьютера!

3. Запустите программу L-phys.ехе, выберите пункт меню «СПИСОК РАБОТ» и в появившемсяна экране списке выберите лабораторную работу «Измерение скорости тела методом бал­листического маятника».

4.  Датчик угла поворота регистрирует углы в интервале 0 ¸ 3600°, т. е. делает 10 оборотов вокруг своей оси, однако наибольшая точность измерений достигается в диапазоне 0 ¸ 360°. Для того, чтобы угол отклонения маятника при измерениях не выходил за рамки указанного интервала, его положение равновесия должно быть в диапазоне углов 90 ¸ 270°. Цифры на экране будет соответствовать текущему значению угла, регистрируемого датчиком. Установите требуемое значение угла положения равновесия, аккуратно вращая маятник вокруг оси датчика и при необходимости, сняв датчик со штатива и повернув его корпус на 180°.

5. Зарядите метательное устройство. Утопите шток, толкающий пульку, внутрь цилиндрической части корпуса. При этом Вы сожмете пружину, которая находится внутри корпуса. После этого вложите пульку в желоб так, чтобы она касалась конца штока.

66

Выберите в меню на экране компьютера пункт «ЗАПУСК». Заряженное метательное устройство расположите вплотную к цилиндру баллистического маятника. Обратите внимание на то, что ось симметрии метательного устройства, определяющая направление скорости движения пульки, во-первых, должна быть горизонтальной и, во-вторых, находиться в плоскости колебаний баллистического маятника. Только при соблюдении указанных условий удар будет прямым и центральным, т. е. будут справедливы соотношения, использованные выше при выводе расчетной формулы. Интервал времени между подачей команды «ЗАПУСК» и выстрелом не должен превышать 5 с, иначе датчик вместо сигнала зарегистрирует шумы.

Произведите выстрел (нажмите кнопку на корпусе метательного устройства) и уберите метательное устройство, чтобы маятник мог беспрепятственно двигаться после возврата в положение равновесия.

Таблица 1