Методические указания к лабораторным работам "Изучение законов сохранения при соударении двух шаров", "Изучение вращательного движения на маховике Обербека", "Изучение закона сохранения момента импульса", "Измерение момента инерции маятника Максвелла", страница 8

Здесь d₁ и d₂ – расстояния от центра масс маятника до рёбер первой и второй призм соответственно; очевидно,что d₁ + d₂ = b (см. рис. 1).

Возведем правые и левые части формул (6) в квадрат и умножим на знаменатели правых частей:

T_ф²mgd₁ = 4p²(I₀ + md₁²),

T_ф²mgd₂ = 4p²(I₀ + md₂²)

Вычтем из первого равенства второе и сократим на m:

T_ф²g(d₁- d₂) = 4p²(d₁² - d₂²),

Оборотный маятник несимметричен, то есть d₁¹ d₂, или, другими словами, d₁ - d₂ ¹ 0. Поэтому мы можем сократить и правую и левую части данного уравнения на разность (d₁- d₂), в результате чего получим:

T_ф²g = 4p²(d₁ + d₂),

или, с учётом того, что d₁ + d₂ = b,  

Т_ф = 2p.                                                  (7)

Из этого выражения следует формула для определения g :

g= 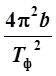                                                (8)

Подчеркнем, что в случае d₁ = d₂ (симметричное расположение осей колебаний относительно центра масс маятника), формулы (7) и (8) не являются справедливыми. Величина периода колебаний в этом случае зависит не только от bи g, но и от момента инерции маятника I₀.

Порядок выполнения работы

27

В данной лабораторной работе с помощью оптодатчика измеряется промежуток време­ни между двумя ближайшими прохождениями груза маятника через положение равновесия, т.е. непосредственно измеряется половина периода колебаний

1. Для проведения опыта с математическим маятником соберите установку как показано на рис. 2. Штатив собирается с длинной вертикальной стойкой (1), к которой крепится кронштейн (2). На конце кронштейна гайкой (3) зажимается шайба, к которой привязана нить с шариком (4). Высота расположения кронштейна (2) подбирается такой, чтобы центр шарика находился на одной высоте с излучателем и приемником оптодатчика (5). Оптическая ось датчика должна приблизительно совпадать с положением равновесия маятника.

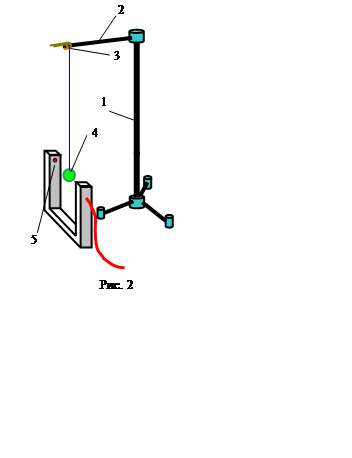
2. Подключите измерительный блок L-микро к разъему последовательного порта компьютера. После этого подсоедините его к сети (220 В, 50 Гц) и включите. Оптодатчик подключается к первому каналу измерительного блока (рис. 3).

3. Запустите программу L-рhys.ехе, выберите пункт «СПИСОК ОПЫТОВ» и в появившемся на экране списке выберите лабораторную работу «Определение ускорения свободного падения».

4. При проведении опытов (как с математическим, так и с оборотным маятниками) необходимо привести маятник в движение и выбрать пункт меню «ИЗМЕРЕНИЕ». После совершения маятником пяти полных колебаний автоматическая запись данных прекращается, а на экране остаётся таблица полупериодов колебаний. Возможная разница между полупериодами Т_0,5 и Т_0,5¢, измеренными при движении маятника в одну и другую стороны, объясняется тем, что оптическая ось датчика не точно совпадает с положением равновесия маятника.

5. Измерьте период малых колебаний математического маятника. Для этого проведите измерения подупериодов при двух различных амплитудах колебаний, достаточно малых с тем, чтобы период не зависел от амплитуды (в рамках точности измери­тельной системы). Измеренные значения Т_0,5 и Т_0,5¢ колебаний внесите в таблицу 1; туда же запишите рассчитанные значения периодов колебаний маятника.

Измерьте линейкой расстояние lот центра шарика до точки подвеса и впишите полученное значение в таблицу 1.

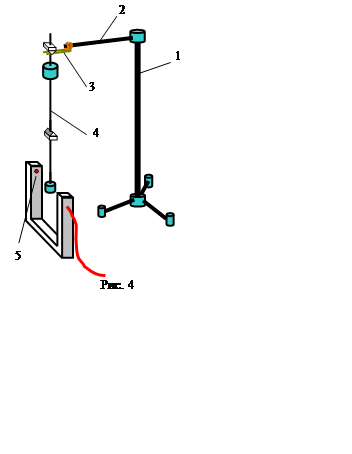6. Положите маятник горизонтально на какой-либо острый предмет (например, ребро линейки) и найдите приблизительно положение центра масс - точку, опираясь на которую маятник будет в равновесии. Проверьте, выполняется ли условие d₁ ¹ d₂ применимости формулы (8).

28

29

7. Для проведения измерений с оборотным маятником на конце кронштейна (1) с помощью двух гаек (2) закрепляется скоба (3) (рис. 4). Оборотный маятник (4) вставляется в прорезь скобы таким образом, чтобы плоскость его колебаний совпадала с направлением прорези. При движении маятник должен перекрывать луч света в оптодатчике (5), установленном на столе. Необходимо, чтобы оптическая ось датчика примерно совпадала с положением равновесия маятника. Высота расположения оси маятника регулируется перемещением кронштейна (2) по вертикальной стойке штатива (1).

Таблица 1

№ опыта	Полупериод Т0,5, с	Полупериод Т0,5¢, с	Период Т, с	Среднее значение периода ТСР, с	Ошибка D Т измерения периода, с
1.
2.
Длина маятника l, м:

Таблица 2

№ опыта		Полупериод Т0,5, с	Полупериод Т0,5¢, с	Период Т, с	Среднее значение периода ТСР, с	Ошибка DТ измерения периода, с
Призма 1	1.
	2.
Призма 2	1.
	2.
Расстояние между вершинами призм b, м: