Методические указания к лабораторным работам "Изучение законов сохранения при соударении двух шаров", "Изучение вращательного движения на маховике Обербека", "Изучение закона сохранения момента импульса", "Измерение момента инерции маятника Максвелла", страница 15

Экспериментально коэффициент внутреннего трения жидкости может быть найден путем измерения силы трения, возникающей при падении твердого тела (например, шарика) в этой жидкости. Различие скоростей слоев жидкости возникает потому, что в результате взаимного притяжения между частицами жидкости и падающего твердого тела (шарика) ближайший к шарику слой движется со скоростью шарика, а остальные – со все уменьшающейся скоростью. Слой жидкости, примыкающий к стенкам сосуда, имеет скорость, равную нулю.

Величину силы трения можно определить следующим образом.

На твердый шарик, падающий в жидкости, действует три силы (см. рис. 2):

- 

55

Сила тяжести , направленная вертикально вниз, причём

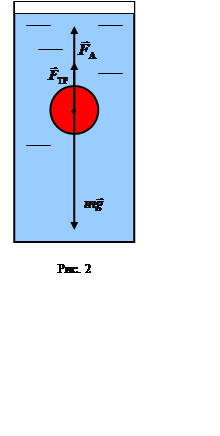mg = pr³r₁g ,(2)

где m– масса шарика;

        r – его радиус;

  r₁ – плотность материала шарика при данной температуре;

  g – ускорение свободного падения.

-  Подъемная сила Архимеда , направленная вертикально вверх и равная весу жидкости, вытесненной шариком,

F_A= pr³r₂g ,(3)

Здесь r₂ – плотность жидкости при данной температуре.

-  Сила трения , направленная в сторону, обратную скорости движения (в нашем случае вертикально вверх), и пропорциональная при малых скоростях величине скорости. Как показал Стокс, эта сила при движении твердого тела, имеющего шаровую форму, равна

F_ТР = 6phu,(4)

где u  – скорость движения шарика;

 h – искомый коэффициент внутреннего трения.

В результате действия на шарик трех сил он будет двигаться под действием их равнодействующей F. Согласно формулам (2) – (4),

F = P - F_А - F_ТР  .

Силы mg и F_А постоянны, а F_ТР  растет с увеличением скорости шарика. Это приводит к тому, что равнодействующая данных сил будет уменьшаться до тех пор, пока не станет равной нулю:

F= mg- F_А - F_ТР  = 0 .(5)

56

Начиная с этого момента, шарик будет двигаться равномерно. Подставляя значения действующих сил, а также формулы (2), (3) и (4) в выражение (5), получим условие равномерности движения шарика в виде

pr³g(r₂-r₁) - 6phu= 0,

откуда может быть определено значение h.

Подставляя в это уравнение скорость установившегося равномерного движения u=  (здесь l– путь, который проходит шарик за время t) и учитывая, что диаметр шарика d = 2r, получаем окончательное выражение для расчета коэффициента внутреннего трения жидкости:

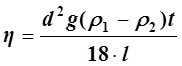.                                   (6)

Порядок выполнения работы

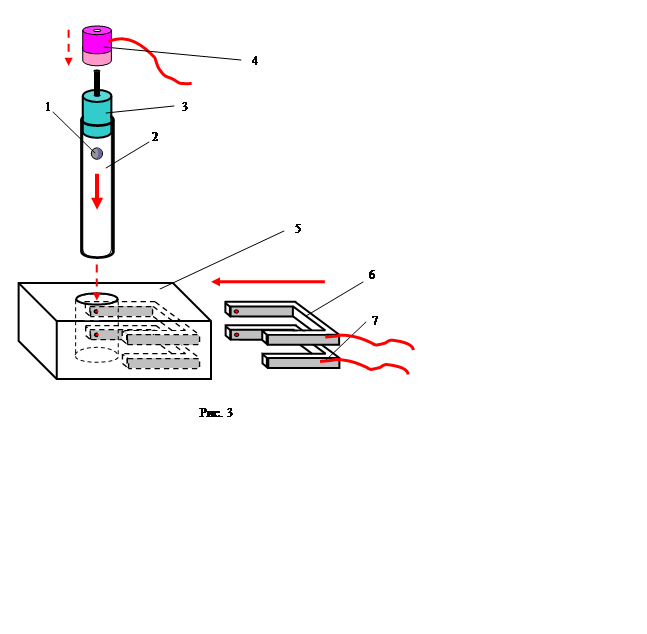
1.  Соберите установку для измерения вяз­кости как показано на рис. 3. Шарик (1) диаметром d , изготовленный из стали плотностью r₁ уже находится в трубке (2), заполненной жидкостью с плотностью r₂. В верхнюю часть трубки вставлена пробка с металлическим стержнем (3), выходящим из пробки наружу. На этом стержне закрепляется катушка электромагнита (4), который необходим, чтобы удерживать шарик. Трубка вводится в цилиндрический канал специального основания (5), имеющего боковые прорези для оптодатчиков (6) и (7). Оптодатчики необходимо вставить в данные прорези.

После отключения питания электромагнита шарик падает вниз; в работе автоматически измеряется время t между срабатываниями верхнего и нижнего датчиков, оптические оси которых расположены на расстоянии l друг от друга.

57

2. Подключите измерительный блок L-микро к разъему последовательного  порта компьютера и включите его в сеть (220В, 50Гц). Девятиштырьковый разъем кабеля электромагнита подсоедините к третьему каналу измери­тельного блока, а на два штекера этого кабеля подайте постоянное напряжение 6В от блока питания. В первый и второй каналы измерительного блока включите оптодатчики (рис. 4). Включите измерительный блок L-микро.

 

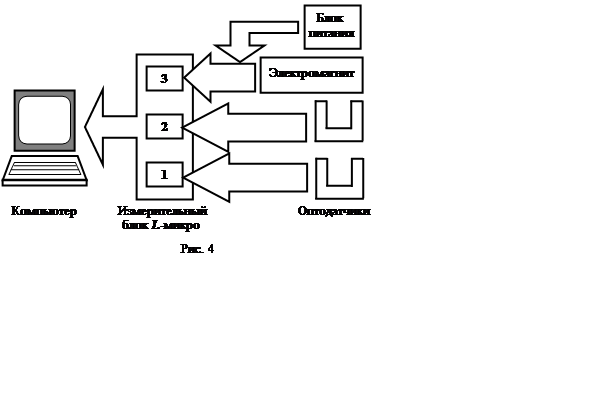
3. Запустите программу L-рhуs.ехе, выбе­рите пункт меню «СПИСОК ОПЫТОВ» и в поя­вившемся на экране списке выберите лаборатор­ную работу «Измерение вязкости жидкости методом Стокса».

4. Выберите пункт меню «ИЗМЕ­РЕНИЕ», при этом будет подано напря­жение питания на электромагнит. Пере­верните трубку с жидкостью для того, чтобы шарик захватился электромагни­том. Вставьте трубку обратно в основание и произведите запуск (отключите питание электромагнита нажатием клавиши на экране). Время пролета шарика между оптическими осями датчиков появится на экране дисплея.

58

5. Проведите опыт 10 раз. Результаты измерений запишите в таблицу 1.

Внимание: иногда шарик падает не по оси цилиндра с жидкостью, а проходит ближе к стенке. В этом случае его движение не регистрируется оптодатчиками, и, следовательно, опыт необходимо повторить.

Таблица 1

№	1	2	3	4	5	6	7	8	9	10
t, с

6. Вычислите усредненное значение времени движения шарика между оптодат­чиками t_СР. Используя известное значение расстояния, которое шарик пролетает  между оптическими осями датчиков за время t_СР, вычислите скорость шарика u. Результаты вычислений запишите в таблицу 2.В эту таблицу уже внесены значения диаметра d шарика, его плотности r₁и плотности жидкости r₂, а также – расстояния lмежду оптическими осями датчиков.

Таблица 2

d, м	r1 , кг/м3	r2 , кг/м3	l, м	tСР, с	u, м/с
0,0051	7,8×103	1,18×103	0,03