Физика \ Физика

Методические указания к лабораторным работам "Изучение законов сохранения при соударении двух шаров", "Изучение вращательного движения на маховике Обербека", "Изучение закона сохранения момента импульса", "Измерение момента инерции маятника Максвелла", страница 4

*Диаметры, м* *больших шаров*		*Диаметр* D₃, м малого шара	*Масса* m₁, кг большого шара	*Масса* m₁, кг малого шара
D₁=	D₂=		*0,02520*	*0,00425*
DD, м – приборная ошибка *измерения диаметров шаров*			Dm₁, кг - ошибка измерения m₁	Dm₁, кг - ошибка измерения m₁

9. Рассчитайте ошибки измерения скоростей шаров в обеих сериях экспериментов. Поскольку измерения скорости – косвенные, и преобладающей является ошибка измерения времени, фиксируемого оптодатчиками, соответствующие ошибки рассчитываются как среднеквадратичные.

Среднеквадратичная ошибка s_fизмерения какого-либо параметра f =f(x, y, z…) в общем виде рассчитывается по формуле

s_f=.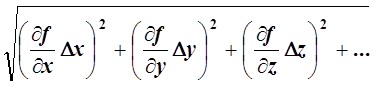

Поскольку в настоящей работе скорости шаров вычисляются через измерения их диаметра и времени пролёта мимо оптодатчика, в каждом случае ошибка рассчитывается по одной и той же формуле: меняются лишь значения ошибок измерения диаметров DD и времён Dt₁, Dt₂,Dt₁¢,Dt₂¢и Dt₃ соответственно. Обозначив в общем случае ошибку измерения скорости символом s_u, а ошибку измерения времени – символом Dt₃, можно записать:

s_u=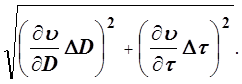

Продифференцировав выражение (10) для расчёта скорости шаров по Dиt, а также использовав вычисленные на предыдущем этапе значения t_СР, после стандартных преобразований можно получить необходимую формулу для расчёта :

s_u=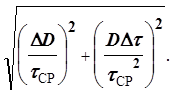

В этой формуле DD – приборная ошибка штангенциркуля для измеренияD; Dt – случайная ошибка измерения времени оптодатчиком, которая рассчитывается по формуле

Dt= a .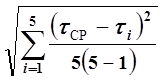

Здесь a-коэффициент Стьюдента, значения которого можно найти в таблице, приведённой в Приложении к настоящему сборнику (см. также методические указания [3]). Величину доверительной вероятности при выборе коэффициента Стьюдента по этой таблице примите равной 0,95.

10. Округлите полученные ошибки до первой значащей цифры; до этого же разряда округлите полученные ранее значения средних скоростей шаров (п. 8). Результаты измерений представьте в виде:

u₁=u_1СР ± s_u₁

u₂=u_2СР ± s_u2

u₁¢=u₁¢_СР ± s¢_u₁

u₁¢=u₁¢_СР ± s¢_u1

u₂¢=u₂¢_СР ± s¢_u2

Контрольные вопросы

1. Какие законы сохранения Вам известны? Приведите формулировки законов сохранения в механике.

2. Сформулируйте и приведите формулу второго закона Ньютона. Покажите, какой вид примет формула, если предположить, что масса тела не меняется в процессе его движения.

3. Покажите, что если шары имеют одинаковую массу, то после соударения с покоящимся шаром налетающий шар остановится, а покоившийся приобретёт ту же скорость, с которой двигался первый шар.

4. Объясните, как рассчитывается доля механической энергии, теряемой шарами при соударении.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1. Савельев И. В. Курс общей физики: В 3-х т. – М.: Наука, 1987. – Т. 1, 432 с.

2. Яворский Б.М., Детлаф А.А. Курс физики. – М.: Высш. шк., 2000.

3. Расчет погрешностей в лабораторных работах физического практикума. Методические указания к вводным занятиям в физическом практикуме/ Н.А. Гринчар, Ф.П. Денисов, Б.А. Курбатов и др.; Под общ. ред. Ф.П. Денисова. - М.: МИИТ, 1995. - 38 с.

4. Методические указания к лабораторным работам по физике. Работы 60-63. Ошибки измерения физических величин. - М.: Изд. МИИТ, 1976. - с. 10 -11.

РАБОТА № 3-П

ИЗУЧЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА МАХОВИКЕ ОБЕРБЕКА

Цель работы: Измерение момента инерциитвердых тел, исследование зависимости момента инерции от формы тела.

Приборы и принадлежности: маховик Обербека, набор грузов, штатив универсальный, линейка, штангенциркуль, датчик угловой скорости с муфтой, измерительный блок L-микро.

Введение

В лабораторной работе рассматривается вращательное движение устройства, которое исторически получило название маховика Обербека.

Для описания вращательного движения, как и для описания поступательного движения, используется ряд параметров, определения некоторых из которых приведены в таблице 1

Таблица 1

ПАРАМЕТРЫ, ХАРАКТЕРИЗУЮЩИЕ ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ПО ПРЯМОЙ	ПАРАМЕТРЫ, ХАРАКТЕРИЗУЮЩИЕ ПЛОСКОЕ ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ
D - перемещение (x - координата)	- угол поворота j - величина угла поворота
- скорость;	- угловая скорость;

- ускорение;	- угловое ускорение;

- импульс	- момент импульса отн. точки; L = r×p×sin a
- сила	= - момент силы отн. точки; M = r×F×sin a
M - масса	I = Sm_i r_i²– момент инерции