Методические указания к лабораторным работам "Изучение законов сохранения при соударении двух шаров", "Изучение вращательного движения на маховике Обербека", "Изучение закона сохранения момента импульса", "Измерение момента инерции маятника Максвелла", страница 11

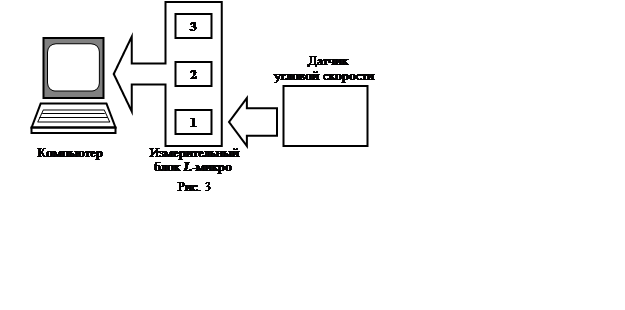
в) Включите режим регистрации данных компьютером. Для этого выберите пункт меню «запуск»  (Отметим, что запись данных осуществляется в течение 20 секунд с момента выбора пункта меню).

г) Раскрутите систему грузов с помощью специального устройства (7) и резко поднимите его вверх, чтобы позволить грузам сдвинуться до резиновых шайб, ограничивающих их движение по стержням (4). Добейтесь того, чтобы после разлёта грузы останавливались на одинаковом расстоянии r₂от оси вращения, не застревая по дороге и не отскакивая от упоров.

39

д) После завершения записи данных на экране компьютера появится график зависимости угловой скорости вращения системы от времени. Вам следует определить w₁ – значение угловой скорости до того как грузы начнут разлетаться и w₂ – значение угловой скорости системы с грузами, переставшими скользить по спицам. Для этого с помощью компьютерной мыши подведите курсор (вертикальную черту) к соответствующим точкам графика и выпишите в таблицу 2. значения угловых скоростей (цифры в верхней части экрана).

Таблица 1 

Н, м	R1 , м	R2, м	m1, кг	m2, кг
0,019	0,014	0,003

Начальной скоростью вращения системы следует считать максимальное значение угловой скорости. Участок возрастания угловой скорости на графике соответствует раскрутке системы, а участок, где угловая скорость убывает – разлету грузов, то есть – движению в отсутствие внешних сил. (Моментом сил трения пренебрегаем.)

Таблица 2

№	r1, м	r2 , м	w1, рад/с	Dw1, рад/с	w2, рад/с	Dw2, рад/с	I1+I2, кг×м2	I1¢+I2¢, кг×м2
1
2
3
4
5
6
7
8
9

40

Измерения необходимо провести при одинаковых начальных (r₁) и трёх различных конечных положениях r₂ ограничительных резиновых шайб, каждый раз проводя по 3 запуска системы (итого – 9 измерений).

5. Используя данные экспериментов (см. таблицу 1), вычислите значения совокупных моментов инерции грузов I₁ +I₂и I₁¢ +I₂¢соответственно до и после разлёта. Грузы можно считать однородными цилиндрами, вращающимися относительно оси, параллельной той, которая проходит через центр масс цилиндра перпендикулярно его оси симметрии.

При расчётах следует применить теорему Штейнера: момент инерции тела I относительно произвольной оси равен сумме момента инерции I₀ относительно оси, парал­лельной данной и проходящей через центр масс тела, и произведения массы тела т на квадрат расстояния d  между осями:

I = I₀ + md².                                          (7)

В нашем случае расстояния между осями OO¢и АА¢(или ВВ¢) – см. рис. 1, – OO¢и СС¢, OO¢и DD¢,равны r₁, и r₂ соответственно, причём момент инерции Iгруза – полого цилиндра с внешним радиусом R₁, внутренним радиусом R₂, высотой Н и массой m относительно оси АА¢рассчитывается по формуле:

I=(3R₁² + 3R₂² + H²).                               (8)

Значения m, R₁ , R₂ и Н возьмите из таблицы 1.

Таким образом, момент инерции грузов до разлёта вычисляется по формуле

I₁ + I₂= (m₁+ m₂)[(3R₁² + 3R₂² +H²) + r₁²],          (9)

а после разлёта – по формуле

I₁ ¢+ I₂¢= (m₁+ m₂)[(3R₁² + 3R₂² +H²) + r₂²].      (10)

Результаты расчётов запишите в таблицу 2.

41

6. Учтём теперь, что момент инерции стержней, по которым скользят грузы, и находящейся на оси датчика угловой скорости муфты, к которой эти стержни крепятся, по величине сопоставим с моментом инерции подвижных грузов, и поэтому его необходимо учитывать при обработке данных эксперимента. Момент инерции I_П подвижной (без грузов) части установки следует вычислить, исходя из теоретических соображений. Значение момента инерции муфты I_М и её радиуса R_Мприведено в таблице 3; момент инерции стержней – цилиндров длиной l, массой m₀ (также см. таблицу 3) может быть рассчитан следующим образом.

Таблица 3 

IМ, кг×м2	RМ, м	l, м	т0, кг	IС , кг×м2	IП, кг×м2
0,000002	0,0125	0,160	0,032

Момент инерции спицы – тонкого однородного стержня относительно оси, проходящей через центр масс стержня перпендикулярно стержню, рассчитывается по формуле

I=m₀l² .                                          (11)

В нашем случае спицы вращаются относительно другой оси - ОО¢, которая сдвинута от той, для которой получена формула (9), на расстояние

d=R_М+.

Расчёт момента инерции относительно этой оси можно выполнить с помощью теорема Штейнера:

I_С  = m₀l² + m₀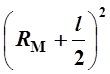,                            (12)

и, следовательно, – вычислить момент инерции I_П всей подвижной части без грузов: муфты и двух спиц:

I_П  = I_М + 2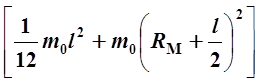.                    (13)

Результаты вычислений запишите в таблицу 3.

42

При расчётах I_С и I_П следует сохранять столько же знаков после запятой, сколько их содержит I_М.

7. Пользуясь формулой (5), а также данными таблиц 2 и 3, рассчитайте значения моментов импульса L_iсистемы (включающей в себя муфту, спицы и грузы) до разлёта грузов и L_i¢ - после их разлёта. Результаты запишите в таблицу 4.

Таблица 4

№	1	2	3	4	5	6	7	8	9	средние
L,  кг×м2×с- 1
L¢,  кг×м2×с- 1