Назначение лазерного резонатора, виды потерь в лазерном резонаторе. Число Френеля и его физический смысл. Добротность лазерного резонатора и её связь с потерями в резонаторе. Добротность резонатора и её связь с полосой пропускания

Примечания:

Вопрос про число Френеля – разбиение на зоны Френеля см. в методичке стр.14, там большой нудный текст и картинка, но достаточно его один раз посмотреть

Неустойчивый телескопический конфокальный – см. рисунок стр 60

Добротность + полоса пропускания – см рисунок стр.21

Типы резонаторов – таблица стр.26

Устойчивость – см рисунок стр 28

Формирование стоячих волн – рисунок стр 35,

Моды – рисунок 1 – стр 38,

Классификация мод – рисунок стр. 42

Частотный спектр – рисунок стр 44

Конфокальный и его моды – рисунок 1 стр 50

Билет №1

1.  Назначение лазерного резонатора, виды потерь в лазерном резонаторе

Как известно, активная среда, находясь в состоянии с инверсной населенностью, способна усиливать проходящее через неё излучение. Однако если бы излучение проходило через активную среду один раз, то мощность выходящего излучения была бы небольшой. Кроме того, оно не имело бы преимущественного направления распространения. Поэтому основным назначением резонатора лазера является создание таких условий, при которых возникающее внутри него индуцированное излучение многократно проходит через активную среду. Это достигается выбором определенного взаимного расположения зеркал резонатора (юстировкой).

Резонатор в значительной степени определяет свойства  выходного лазерного излучения. Направленность процесса усиления волн полностью зависит от конфигурации резонатора – от размера и формы его зеркал и расстояния между ними. Поэтому геометрия резонатора определяет направленность выходного излучения, угол его расходимости и вообще все пространственные характеристики лазерного пучка. Но также она определяет и частотный спектр излучения, делая лазер одномодовым, многомодовым или одночастотным. Таким образом, когерентные свойства пучка, как временные, так и пространственные, определяются в конечном итоге геометрией резонатора лазера.

              Рассмотрим плоскопараллельный резонатор, в котором расстояние между зеркалами равно. Введем в пространстве резонатора систему декартовых координат, так чтобы ее центр совпадал с центром первого зеркала, а поверхность этого зеркала лежала в плоскости . Тогда ось будет перпендикулярна обоим зеркалам и становится осью резонатора. При распространении излучения от зеркала к зеркалу оно испытывает потери энергии связанные с её поглощением, рассеянием, пропусканием зеркал, дифракцией, неточностью юстировки и пр.  Математически влияние этих потерь можно учесть в уравнении баланса

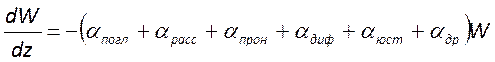, которое также часто записывается не для энергии, а для интенсивности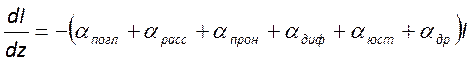

Здесь

- показатель потерь, обусловленных поглощением излучения поверхностью зеркал и средой

- …обусловленных процессом рассеяния излучения

-…, обусловленных пропусканием зеркал, из-за чего излучение выводится из резонатора и используется по назначению

- …, обусловленных дифракцией излучения на зеркалах и внутрирезонаторных эл-тах

-…, обусловленных неточностью юстировки

- показатель других видов потерь.

Следует подчеркнуть, что различные виды потерь носят разный характер. Например, процессы поглощения и рассеяния всегда являются вредными, а потери от пропускания зеркал следует всегда считать полезными.

Иногда наряду с показателем потерь вводится безразмерный коэффициент потерь излучения на одном проходе излучения . И для различных видов потерь этот коэффициент принимает следующий вид

; ;

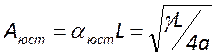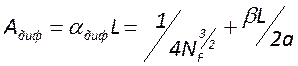
В теории резонаторов дифракционные потери играют основную роль, так как другие виды потерь, в основном, влияют на мощность излучения, а дифракционные потери влияют на частотные фазовые и пространственные характеристики.

2.  Эквивалентный конфокальный резонатор.

Метод эквивалентного конфокального резонатора (ЭКР) применяется в качестве первого приближения, пригодного для оценок распределения собственного поля резонатора, его спектра и потерь.

Метод заключается в предположение, что для каждого произвольного резонатора можно найти такой воображаемый  конфокальный резонатор, в наборе волновых поверхностей которого найдутся две, совпадающие по кривизне и расстоянию друг от  друга с отражающими поверхностями исходного резонатора. Это и будет ЭКР. При этом полагают, что расстояние между зеркалами  является конфокальным параметром рассматриваемого произвольного резонатора.

В основе метода ЭКР лежит предположение о том, что поле рассматриваемого резонатора идентично по своим свойствам полю , и может быть описано через его параметры. ЭКР определяется своей длиной () и местоположением перетяжки относительного зеркал рассматриваемого резонатора (). Исходная система уравнений записывается в виде

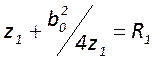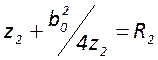; ; (1)

Решая систему (1), находим параметры ЭКР

;;

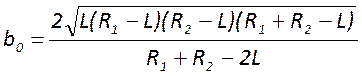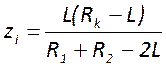Здесь положительно, если перетяжка находится от i -го зеркала со стороны резонатора . Другие геометрические параметры пучка :

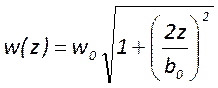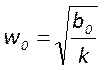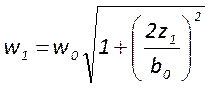; ; и 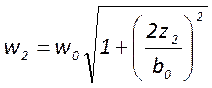- размеры пятен на зеркалах резонатора

При введении метода ЭКР предполагается, что потери рассматриваемого резонатора равны потерям ЭКР. Это предположение будет верно, если дифракционные потери малы.

Для частотного спектра ЭКР имеет место формула

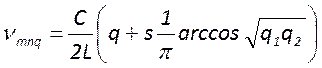, где для прямоугольной симметрии резонатора , а для цилиндрической

Билет №2

1.  Число Френеля и его физический смысл

Пусть в плоскопараллельном резонаторе световая волна, отраженная от первого зеркала, дифрагирует в угол, который называется дифракционным и имеет величину

Чем меньше этот угол по сравнению с углом поля зрения  - углом, под которым второе зеркало видно из центра первого, тем  эффективнее второе зеркало получает излучение, тем меньше буду потери за счет дифракции. Угол поля зрения можно выразить как 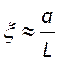, если . Тогда для уменьшения дифракц. потерь  требуется выполнение условия или 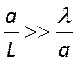. Запишем это условие в несколько ином виде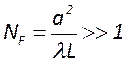

Безразмерная величина называется числом Френеля, которое является важным физическим параметром резонатора и определяет многие его свойства.  Чтобы выяснить его физический смысл, проведем разбиение отражающей поверхности  второго зеркала на зоны Френеля, которые наблюдаются из центра первого зеркала (разбиение)

Важным свойством зон Френеля является то, что они примерно равны по площади. Действительно, площадь центрального круга

А площадь первого кольца

Вообще площадь n-го кольца

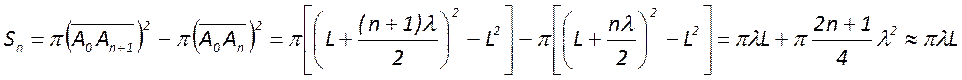Отсюда следует, что равенство площадей будет выполняться, пока выполняется условие

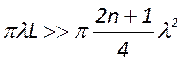или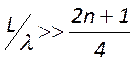

Вычислим полное число зон Френеля, умещающихся на поверхности второго зеркала

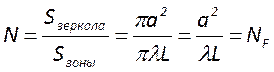. Отсюда следует, что физический смысл числа Френеля состоит в том, что оно есть число зон Френеля, наблюдаемых на поверхности одного зеркала конечной апертуры из центра другого зеркала. Однако применительно к лазерной физике его стоит трактовать по-другому. Изначально мы определили число Френеля как отношения угла поля зрения к углу дифракции. Смысл этого отношения в том, что оно будет определять  наибольшее число проходов излучения через активную среду лазера, т.е число актов усиления.

2.  Полуконфокальный резонатор и частотный спектр его мод.

В настоящее время наибольшую распространенность получили так называемые полуконфокальные резонаторы, у которых одно зеркало является плоским , а второе имеет радиус  и его фокус лежит на плоском зеркале.