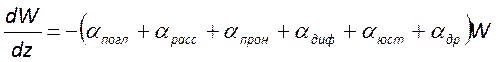Назначение лазерного резонатора, виды потерь в лазерном резонаторе. Число Френеля и его физический смысл. Добротность лазерного резонатора и её связь с потерями в резонаторе. Добротность резонатора и её связь с полосой пропускания, страница 14

, которое также часто записывается не для энергии, а для интенсивности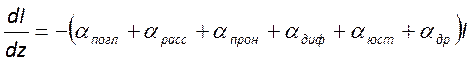

Здесь

- показатель потерь, обусловленных поглощением излучения поверхностью зеркал и средой

- …обусловленных процессом рассеяния излучения

-…, обусловленных пропусканием зеркал, из-за чего излучение выводится из резонатора и используется по назначению

- …, обусловленных дифракцией излучения на зеркалах и внутрирезонаторных эл-тах

-…, обусловленных неточностью юстировки

- показатель других видов потерь.

Следует подчеркнуть, что различные виды потерь носят разный характер. Например, процессы поглощения и рассеяния всегда являются вредными, а потери от пропускания зеркал следует всегда считать полезными.

Иногда наряду с показателем потерь вводится безразмерный коэффициент потерь излучения на одном проходе излучения . И для различных видов потерь этот коэффициент принимает следующий вид

; ;

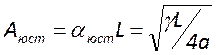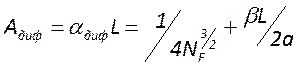
В теории резонаторов дифракционные потери играют основную роль, так как другие виды потерь, в основном, влияют на мощность излучения, а дифракционные потери влияют на частотные фазовые и пространственные характеристики.

Билет №23

1.  Добротность резонатора и её связь с полосой пропускания.

Универсальным параметром, характеризующим накопительные свойства резонатора, является его добротность. Она определяется как величина, обратно пропорциональная скорости уменьшения энергии поля в резонаторе. Аналитически её выражают в виде отношения запасенной в резонаторе энергии к энергии, теряемой им за один период колебаний Т..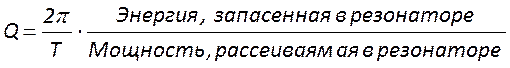

Воспользуемся этим выражением и получим конкретные формулы для добротности резонатора лазера.

Пусть в резонаторе объемом имеет место собственное колебание на частоте . Пусть в начальный момент времени  в этой моде запасена энергия поля , где  - начальная объемная плотность этой энергии. При распространении от зеркала к зеркалу вдоль оси резонатора  данная мода испытывает потери своей энергии.  Обозначив суммарные потери коэффициентом 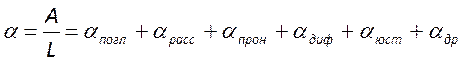, приведем уравнение баланса энергии 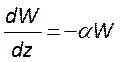 к следующему виду 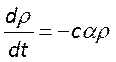.Перепишем ур-е баланса энергии резонат. так чтобы в нём в явном виде содержалась добротность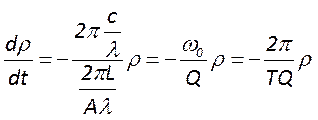

Легко видеть, что решение этого уравнения имеет вид 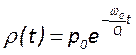. Домножая обе части на объем резонатора , получаем выражение для затухания энергии во времени .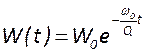

Так как нам известно, изменение энергии резонатора во времени, можно получить выражение для изменения во времени напряженности его поля: 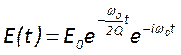. Используя преобразование Фурье можно записать 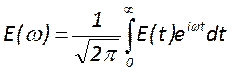.Функция представляет собой спектральное разложение внутрирезонаторного поля. Вычислим эту функцию, подставив в неё выр-е для

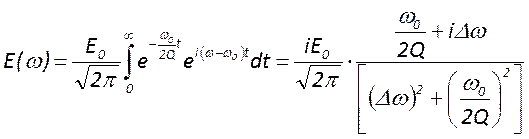, где

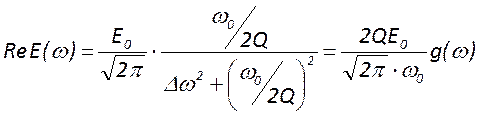- амплитуда

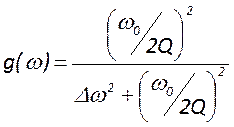- закон изменения амплитуды при изменении частоты. График его имеет вид нормированной кривой (рисунок) и лоренцеву форму. Ширина это линий, определенная на полувысоте равна 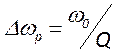 и называется полосой пропускания резонатора.

Таким образом, чем выше добротность резонатора, чем ниже его потери, тем меньше ширина соответствующей резонансной кривой и тем выше амплитуда поля соответствующей моды. Определение полосы пропускания позволяет получить формулу для нахождения добротности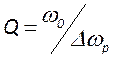

2.  Устойчивость работы резонаторов. Условие устойчивости и его анализ

Резонатор называется устойчивым, если при многократных проходах излучения между зеркалами электромагнитное поле имеет стационарный характер, а его распределение воспроизводится идентично. Это означает, что излучение не выходит за пределы зеркал в поперечном направлении и выводится только благодаря частичному пропусканию зеркал. Поэтому в устойчивом резонаторе, в случае отсутствие потерь, излучение могло бы существовать бесконечно долго. В неустойчивом резонаторе световые пучки в результате последовательных отражений от зеркал  перемещаются в поперечном направлении от оси резонатора к его периферии и покидают его.

Условие устойчивости работы резонатора может быть записано в виде, где 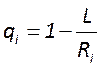- обобщенные параметры резонатора. На рисунке это условие представлено в графическом виде в q-координатах, что позволило наглядно представить область устойчивой и неустойчиво работы резонатора. График позволяет дать обобщенный анализ устойчивости работы резонаторов всех типов. Для этого обычно проводят биссектрису углов 1 и 3 четвертей координатной плоскости и рассматривают те типы резонаторов, параметры которых соответствуют точкам, лежащим на этой биссектрисе. Так как для точек на ней справедливо выполнение равенства , из которого следует равенство , то соответствующие резонаторы называются симметричными. При анализе графика можно сделать следующие выводы

19.  В области отрезка диаметр кривизны зеркал резонатора всегда меньше его длины , поэтому такой тип резонатора всегда будет неустойчивым, так как излучение быстро покидает внутрирезонаторную область через открытую боковую поверхность.

20.  В точке диаметр кривизны поверхности равен длине резонатора . Здесь резонатор становится устойчивым концентрическим

21.  В точке 0 мы имеем устойчивый симметричный конфокальный резонатор

22.  В точке зеркала становятся  плоскими, что соответствует устойчивому плоскопараллельному резонатору.

23.  Точки, лежащие на отрезке , соответствуют симметричным резонаторам с выпуклыми зеркалами, так как в этой области что соответствует . Это область неустойчивой работы, так как излучение быстро покидает внутрирезонаторную область через открытую боковую поверхность.

24.  Для несимметричных резонаторов и соответствующие им точки лежат вне биссектрисы. При этом каждому несимметричному резонатору соответствуют две точки, которые расположенные симметрично относительно биссектрисы, и которые переходят друг в друга при перестановке зеркал. Например, точки соответствуют полуконфокальным резонаторам, а точки - полуконцентрическим

Таким образом за исключением конфокального телескопического резонатора все основные типы конфигураций относятся к устойчивым резонаторам.

Билет №24

1.  Добротность лазерного резонатора и её связь с энергией и интенсивностью излучения