Моды резонатора – теперь рассмотрим пустой прямоугольный резонатор с размерами как на рисунке 1. Если он заполнен излучением то оно принимает равновесное распределение, при котором составляющие напряженности его электрического поля можно представить в виде
(1) ![]() ,
,![]()
![]() , где
, где ![]()
![]()
![]() , а
, а![]() -
целые положительные числа. Резонансные частоты таких стоячих волн определяются
формулой
-
целые положительные числа. Резонансные частоты таких стоячих волн определяются
формулой
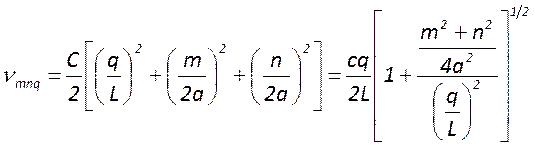 . При этом для каждого набора чисел
. При этом для каждого набора чисел![]() существует вполне определенная мода с
вполне определенной резонансной частотой. Индекс
существует вполне определенная мода с
вполне определенной резонансной частотой. Индекс ![]() равен
числу полуволн укладывающихся на длине резонатора
равен
числу полуволн укладывающихся на длине резонатора ![]() ,
и называется продольным индексом, а индексы
,
и называется продольным индексом, а индексы ![]() и
и ![]() обозначают число изменений знака поля
на поверхности зеркал, и называются поперечными индексами
обозначают число изменений знака поля
на поверхности зеркал, и называются поперечными индексами
Билет №18
1. Устойчивость работы резонаторов. Условие устойчивости и его анализ
Резонатор называется устойчивым, если при многократных проходах излучения между зеркалами электромагнитное поле имеет стационарный характер, а его распределение воспроизводится идентично. Это означает, что излучение не выходит за пределы зеркал в поперечном направлении и выводится только благодаря частичному пропусканию зеркал. Поэтому в устойчивом резонаторе, в случае отсутствие потерь, излучение могло бы существовать бесконечно долго. В неустойчивом резонаторе световые пучки в результате последовательных отражений от зеркал перемещаются в поперечном направлении от оси резонатора к его периферии и покидают его.
Условие устойчивости работы резонатора может быть записано в виде![]() , где
, где 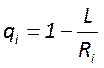 -
обобщенные параметры резонатора. На рисунке это условие представлено в
графическом виде в q-координатах, что позволило
наглядно представить область устойчивой и неустойчиво работы резонатора. График
позволяет дать обобщенный анализ устойчивости работы резонаторов всех типов.
Для этого обычно проводят биссектрису углов 1 и 3 четвертей координатной
плоскости и рассматривают те типы резонаторов, параметры которых соответствуют
точкам, лежащим на этой биссектрисе. Так как для точек на ней справедливо выполнение
равенства
-
обобщенные параметры резонатора. На рисунке это условие представлено в
графическом виде в q-координатах, что позволило
наглядно представить область устойчивой и неустойчиво работы резонатора. График
позволяет дать обобщенный анализ устойчивости работы резонаторов всех типов.
Для этого обычно проводят биссектрису углов 1 и 3 четвертей координатной
плоскости и рассматривают те типы резонаторов, параметры которых соответствуют
точкам, лежащим на этой биссектрисе. Так как для точек на ней справедливо выполнение
равенства ![]() , из которого следует равенство
, из которого следует равенство ![]() , то соответствующие резонаторы
называются симметричными. При анализе графика можно сделать следующие выводы
, то соответствующие резонаторы
называются симметричными. При анализе графика можно сделать следующие выводы
13.
В области отрезка ![]() диаметр кривизны зеркал
резонатора всегда меньше его длины
диаметр кривизны зеркал
резонатора всегда меньше его длины ![]() , поэтому такой
тип резонатора всегда будет неустойчивым, так как излучение быстро покидает
внутрирезонаторную область через открытую боковую поверхность.
, поэтому такой
тип резонатора всегда будет неустойчивым, так как излучение быстро покидает
внутрирезонаторную область через открытую боковую поверхность.
14.
В точке ![]() диаметр кривизны
поверхности равен длине резонатора
диаметр кривизны
поверхности равен длине резонатора ![]() . Здесь резонатор
становится устойчивым концентрическим
. Здесь резонатор
становится устойчивым концентрическим
15. В точке 0 мы имеем устойчивый симметричный конфокальный резонатор
16.
В точке ![]() зеркала становятся
плоскими
зеркала становятся
плоскими![]() , что соответствует устойчивому
плоскопараллельному резонатору.
, что соответствует устойчивому
плоскопараллельному резонатору.
17.
Точки, лежащие на отрезке ![]() , соответствуют
симметричным резонаторам с выпуклыми зеркалами, так как в этой области
, соответствуют
симметричным резонаторам с выпуклыми зеркалами, так как в этой области ![]() что соответствует
что соответствует ![]() . Это область неустойчивой работы,
так как излучение быстро покидает внутрирезонаторную область через открытую
боковую поверхность.
. Это область неустойчивой работы,
так как излучение быстро покидает внутрирезонаторную область через открытую
боковую поверхность.
18.
Для несимметричных резонаторов ![]() и
соответствующие им точки лежат вне биссектрисы. При этом каждому
несимметричному резонатору соответствуют две точки, которые расположенные
симметрично относительно биссектрисы, и которые переходят друг в друга при
перестановке зеркал. Например, точки
и
соответствующие им точки лежат вне биссектрисы. При этом каждому
несимметричному резонатору соответствуют две точки, которые расположенные
симметрично относительно биссектрисы, и которые переходят друг в друга при
перестановке зеркал. Например, точки ![]() соответствуют
полуконфокальным резонаторам, а точки
соответствуют
полуконфокальным резонаторам, а точки ![]() -
полуконцентрическим
-
полуконцентрическим
Таким образом за исключением конфокального телескопического резонатора все основные типы конфигураций относятся к устойчивым резонаторам.
2. Добротность лазерного резонатора и её связь с потерями в резонаторе
Универсальным параметром, характеризующим накопительные свойства резонатора, является его добротность. Она определяется как величина, обратно пропорциональная скорости уменьшения энергии поля в резонаторе. Аналитически её выражают в виде отношения запасенной в резонаторе энергии к энергии, теряемой им за один период колебаний Т.
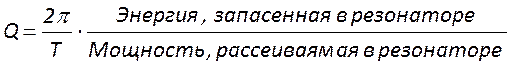 .
.
Воспользуемся этим выражением и получим конкретные формулы для добротности резонатора лазера.
Пусть в резонаторе объемом ![]() имеет место
собственное колебание на частоте
имеет место
собственное колебание на частоте ![]() . Пусть в
начальный момент времени
. Пусть в
начальный момент времени ![]() в этой моде
запасена энергия поля
в этой моде
запасена энергия поля ![]() , где
, где ![]() - начальная объемная плотность этой
энергии. При распространении от зеркала к зеркалу вдоль оси резонатора данная
мода испытывает потери своей энергии. Обозначив суммарные потери коэффициентом
- начальная объемная плотность этой
энергии. При распространении от зеркала к зеркалу вдоль оси резонатора данная
мода испытывает потери своей энергии. Обозначив суммарные потери коэффициентом
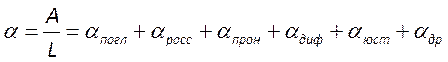 , приведем уравнение баланса энергии
, приведем уравнение баланса энергии 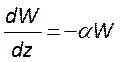 к следующему виду
к следующему виду
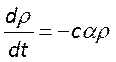 . Интегрированием этого уравнения
получим его решение в виде
. Интегрированием этого уравнения
получим его решение в виде
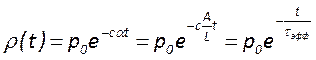 , где
, где 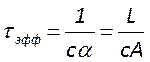 .
.
Это решение свидетельствуем об экспоненциальном характере затухания
моды резонатора с характерным временем ![]() -
временем жизни фотона в моде.
-
временем жизни фотона в моде.
Теперь легко получить выражение для добротности резонатора на частоте
его моды ![]() . Действительно, если запасенная в
начальные момент энергия равна
. Действительно, если запасенная в
начальные момент энергия равна ![]() , а её убыль за
один период колебаний составляет
, а её убыль за
один период колебаний составляет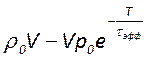 , то получим
, то получим
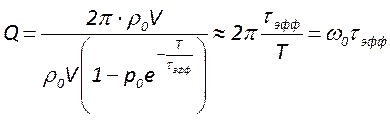 ;
; 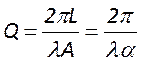 .
Отсюда следует, что чем больше потери резонатора, тем меньше его добротность.
.
Отсюда следует, что чем больше потери резонатора, тем меньше его добротность.
Билет №19
1. Гауссов пучок и его характеристики
Гауссовым называется такой лазерный пучок, который описывается функцией Гаусса. К таким пучкам относятся все, работающие на основной моде. Их особенностью является то, что гауссов пучок преобразуется идеальной тонкой линзой в гауссов же пучок, но с другими параметрами.
Описываются же гауссовы пучки следующими параметрами
Распределение поля гауссова пучка описывается формулой
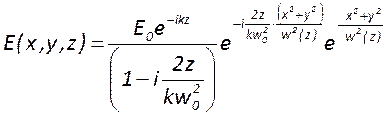
А распределение интенсивности – формулой
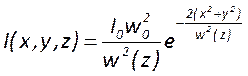 , где
, где ![]() ,
, ![]() и
и ![]() значения
соответствующих величин в точке
значения
соответствующих величин в точке ![]() , а
, а ![]() - значение
- значение ![]() в
плоскости
в
плоскости ![]() . Проведем в некоторой точке
. Проведем в некоторой точке ![]() плоскость, перпендикулярную оси
пучка. Тогда
плоскость, перпендикулярную оси
пучка. Тогда ![]() - радиус пятна пучка в этой
плоскости. На расстоянии
- радиус пятна пучка в этой
плоскости. На расстоянии ![]() от оси пучка
напряженность падает в
от оси пучка
напряженность падает в ![]() а интенсивность в
а интенсивность в ![]() раз. Поверхность одинаковых значений
интенсивности, проведенная на расстоянии
раз. Поверхность одинаковых значений
интенсивности, проведенная на расстоянии ![]() от
пучка, называется каустикой пучка и для гауссова пучка имеет форму поверхности
однополосного гиперболоида вращения. Наиболее узкий участок каустики называется
её перетяжкой, а
от
пучка, называется каустикой пучка и для гауссова пучка имеет форму поверхности
однополосного гиперболоида вращения. Наиболее узкий участок каустики называется
её перетяжкой, а ![]() - радиусом перетяжки. Для
описания гауссовых пучков также вводят параметр
- радиусом перетяжки. Для
описания гауссовых пучков также вводят параметр 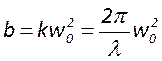 -
конфокальный параметр. Он определяется как высота гиперболоида, площадь торцов
которого в 2 раза больше площади его перетяжки. Другие характеристики,
определяемые для всех видов пучков – радиус кривизны волнового фронта
-
конфокальный параметр. Он определяется как высота гиперболоида, площадь торцов
которого в 2 раза больше площади его перетяжки. Другие характеристики,
определяемые для всех видов пучков – радиус кривизны волнового фронта 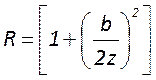 и расходимость луча
и расходимость луча 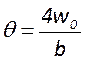
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.