Назначение лазерного резонатора, виды потерь в лазерном резонаторе. Число Френеля и его физический смысл. Добротность лазерного резонатора и её связь с потерями в резонаторе. Добротность резонатора и её связь с полосой пропускания, страница 15

Универсальным параметром, характеризующим накопительные свойства резонатора, является его добротность. Она определяется как величина, обратно пропорциональная скорости уменьшения энергии поля в резонаторе. Аналитически её выражают в виде отношения запасенной в резонаторе энергии к энергии, теряемой им за один период колебаний Т.

.

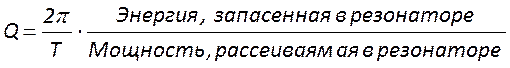Воспользуемся этим выражением и получим конкретные формулы для добротности резонатора лазера.

Пусть в резонаторе объемом имеет место собственное колебание на частоте . Пусть в начальный момент времени  в этой моде запасена энергия поля , где  - начальная объемная плотность этой энергии. При распространении от зеркала к зеркалу вдоль оси резонатора  данная мода испытывает потери своей энергии.  Обозначив суммарные потери коэффициентом 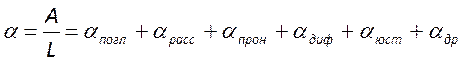, приведем уравнение баланса энергии  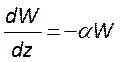к следующему виду

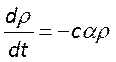
Перепишем уравнение баланса энергии резонатора так, чтобы в нём в явном виде содержалась добротность

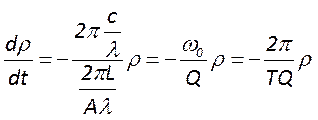                            (1)

Легко видеть, что решение этого уравнения имеет вид 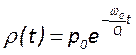. Домножая обе части на объем резонатора , получаем выражение для затухания энергии во времени

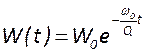. Аналогично решая уравнение баланса интенсивности, получим выражение для её затухания в пространстве .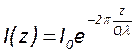

Отсюда следует, что коэффициенты затухания энергии и интенсивности обратно пропорциональны величине добротности.

2.  Число Френеля и его физический смысл

Пусть в плоскопараллельном резонаторе световая волна, отраженная от первого зеркала, дифрагирует в угол, который называется дифракционным и имеет величину

Чем меньше этот угол по сравнению с углом поля зрения  - углом, под которым второе зеркало видно из центра первого, тем  эффективнее второе зеркало получает излучение, тем меньше буду потери за счет дифракции. Угол поля зрения можно выразить как 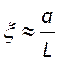, если . Тогда для уменьшения дифракц. потерь  требуется выполнение условия или 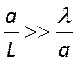. Запишем это условие в несколько ином виде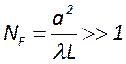

Безразмерная величина называется числом Френеля, которое является важным физическим параметром резонатора и определяет многие его свойства.  Чтобы выяснить его физический смысл, проведем разбиение отражающей поверхности  второго зеркала на зоны Френеля, которые наблюдаются из центра первого зеркала (разбиение)

Важным свойством зон Френеля является то, что они примерно равны по площади. Действительно, площадь центрального круга

А площадь первого кольца

Вообще площадь n-го кольца

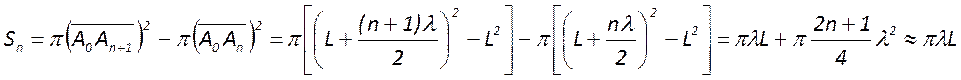Отсюда следует, что равенство площадей будет выполняться, пока выполняется условие

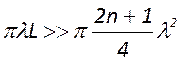или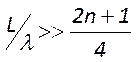

Вычислим полное число зон Френеля, умещающихся на поверхности второго зеркала

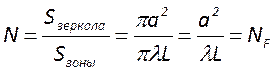. Отсюда следует, что физический смысл числа Френеля состоит в том, что оно есть число зон Френеля, наблюдаемых на поверхности одного зеркала конечной апертуры из центра другого зеркала. Однако применительно к лазерной физике его стоит трактовать по-другому. Изначально мы определили число Френеля как отношения угла поля зрения к углу дифракции. Смысл этого отношения в том, что оно будет определять  наибольшее число проходов излучения через активную среду лазера, т.е число актов усиления.

Билет №25

1.  Добротность лазерного резонатора и её связь с потерями в резонаторе

Универсальным параметром, характеризующим накопительные свойства резонатора, является его добротность. Она определяется как величина, обратно пропорциональная скорости уменьшения энергии поля в резонаторе. Аналитически её выражают в виде отношения запасенной в резонаторе энергии к энергии, теряемой им за один период колебаний Т.

.

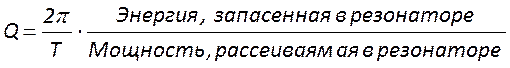Воспользуемся этим выражением и получим конкретные формулы для добротности резонатора лазера.

Пусть в резонаторе объемом имеет место собственное колебание на частоте . Пусть в начальный момент времени  в этой моде запасена энергия поля , где  - начальная объемная плотность этой энергии. При распространении от зеркала к зеркалу вдоль оси резонатора  данная мода испытывает потери своей энергии.  Обозначив суммарные потери коэффициентом 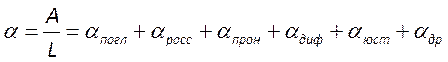, приведем уравнение баланса энергии 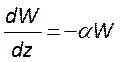к следующему виду

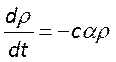. Интегрированием этого уравнения получим его решение в ви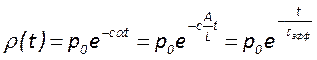де

, где .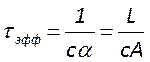

Это решение свидетельствуем об экспоненциальном характере затухания моды резонатора с характерным временем  - временем жизни фотона в моде.

Теперь легко получить выражение для добротности резонатора на частоте его моды . Действительно, если запасенная в начальные момент энергия равна , а её убыль за один период колебаний составляет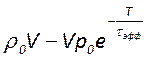, то получим

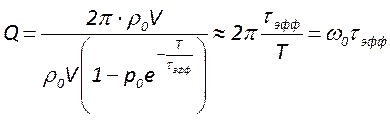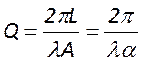; . Отсюда следует, что чем больше потери резонатора, тем меньше его добротность.        

2.  Частотный спектр лазерного излучения и его описание

Частотный интервал между соседними продольными модами, принадлежащими одной поперечной во много раз больше интервала между двумя соседними поперечными. Действительно, интервал между соседними продольными модами

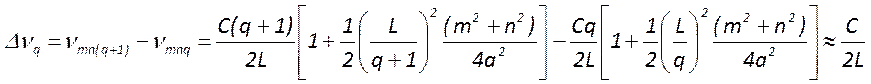, а между соседними поперечными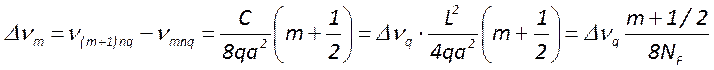

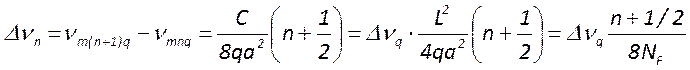
Здесь - число Френеля. Отсюда следует что ;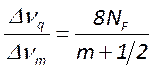

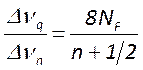
Поскольку для наиболее часто используемых резонаторов , а и имеют величину порядка нескольких единиц, то следует, что .

Для того чтобы определить, сколько резонансных частот будет присутствовать в выходном излучении лазера, необходимо знать ширину контура линии люминесценции рабочего перехода активной среды, так как именно этот диапазон определяет тот спектральный диапазон, в пределах которого осуществляется лазерная генерация. В большинстве случаев выполняется условие и в спектре излучения наблюдается много мод.

На рисунке представлена качественная картина частотного спектра лазерного излучении при использовании плоскопараллельного резонатора.  При этом следует помнить, что спектральные линии излучения, соответствующие модам, будут располагаться по всей ширине линии люминесценции, только если уровень накачки обеспечивает условие  генерации по всему контуру усиления. Если же усиление больше потерь только в определенной области контура, то спектр излучения будет наблюдаться только в этой области.