Назначение лазерного резонатора, виды потерь в лазерном резонаторе. Число Френеля и его физический смысл. Добротность лазерного резонатора и её связь с потерями в резонаторе. Добротность резонатора и её связь с полосой пропускания, страница 6

Таким образом, внутри резонатора поле в каждой точке определяется суммой прямой и обратной волн . Преобразование этих выражений приводит к следующим формулам: ,

Известно, что интенсивность электромагнитной волны определяется вектором Умова-Пойнтинга: 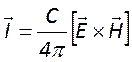. Подставляя сюда найденные выражения, получим абсолютную величину этой интенсивности: 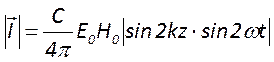. Нетрудно видеть, что данная формула описывает стоячую волну. Действительно, в точках 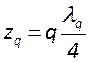интенсивность рассматриваемой волны обращается в ноль, а между ними она принимает ненулевые значения. Это означает, что вся ось резонатора поделена на отрезки длиной , в которых и сосредоточена энергия волны, причем ввиду фиксированности эта энергия не может распространяться, она как бы локализована в пространстве этих отрезков, что характерно только для стоячей волны.

Моды резонатора – теперь рассмотрим пустой прямоугольный резонатор с размерами как на рисунке 1. Если он заполнен излучением то оно принимает равновесное распределение, при котором составляющие напряженности его электрического поля можно представить в виде

(1) ,, где , а- целые положительные числа. Резонансные частоты таких стоячих волн определяются формулой

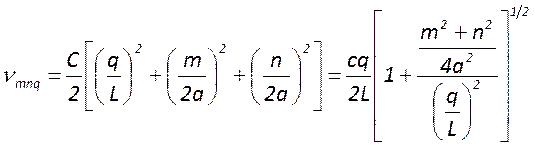. При этом для каждого набора чиселсуществует вполне определенная мода с вполне определенной резонансной частотой. Индекс равен числу полуволн укладывающихся на длине резонатора , и называется продольным индексом, а индексы и обозначают число изменений знака поля на поверхности зеркал, и называются поперечными индексами

2.  Плоскопараллельный резонатор и частотный спектр его мод

Плоскопараллельный – резонатор образованный параллельными плоскими зеркалами. В нём достигается максимальная расходимость пучка по сравнению с другими видами, но наиболее часто он применяется в  тех типах лазеров, которые обладают малой длиной и достаточно хорошим  усилением активной среды, что облегчает его юстировку, поэтому наиболее широко эта конфигурация применяется в твердотельных и полупроводниковых лазерах.

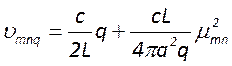Частотный спектр собственных колебаний  плоскопараллельного резонатора с круглыми зеркалами радиуса определяется формулой . Сопоставляя её с общей формулой для резонансных частот 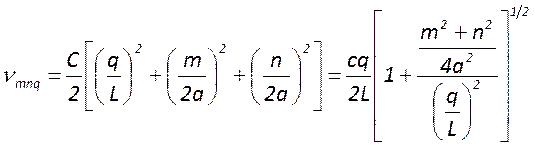, можно сделать вывод, что при имеет место полное совпадение поперечных мод по частотам. В этом случае моды называют частотно вырожденными. При этом можно считать, что в рамках некоторого приближения все поперечные моды плоскопараллельного резонатора частотно вырождены. В этом случае спектр его излучении состоит только из ряда линий, отстоящих друг от друга на частотном расстоянии

Билет №10

1.  Обозначение и классификация мод резонатора

 В теории открытых колебаний типы колебаний принято обозначать как (TEM – аббревиатура от Transverse Electric and Magnetic – Поперечный электрический и магнитный вектор).  Индекс m указывает на количество изменений направления поля вдоль оси x, индекс n – вдоль оси y, индекс q показывает число полуволн, которое укладывается на длине резонатора. Значения индексов выводятся из выражения для резонансной частоты моды резонатора 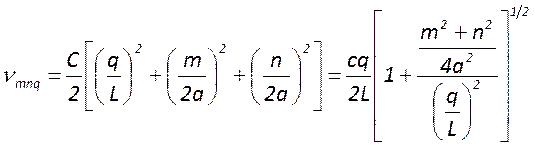.  Такая форма обозначения мод резонатора явилась основой для их классификации. Суть её такова

6.  Мода, у которой поперечные индексы (m,n) фиксированы, а продольный индекс (q) является произвольным – называется поперченной модой. Она включает в себя столько колебаний, сколько принимает значений индекс q. Обозначается она как

7.  Мода, у которой все индексы фиксированы, называется продольной (аксиальной) модой. Она имеет единственную резонансную частоту и является одной из компонент поперечной моды с теми же фиксированными m и n

8.  Поперечная мода с нулевыми поперечными индексами называется основной поперечной модой.

9.  При обозначении поперечной моды для резонатора с прямоугольными зеркалами на первое место ставится тот поперечный индекс, который соответствует большей стороне прямоугольника.

10.  Для круглых зеркал обозначение соответствует цилиндрической системе координат,  поэтому первый индекс обозначает число изменений знака поля по радиусу зеркала, а второй – по углу.

Различия между модами – см рисунок.

2.  Конфокальный резонатор и частотный спектр его мод

Конфокальным называется резонатор образованный совмещением фокусов двух изогнутых зеркал. Особенностью его является то, что поверхности  зеркал являются поверхностями равных фаз, т.е. распределение фазы по поверхности каждого зеркала резонатора. Поле в конфокальном резонаторе сконцентрировано вблизи оси. Важным является то обстоятельство, что потери мощности в таких резонаторах могут быть на несколько порядков меньше чем в плоскопараллельных.

В случае сферических зеркал с квадратной апертурой выражение для собственных частот резонатора принимает простой вид 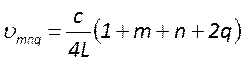. Отсюда следует, что поперечные моды, индексы которых удовлетворяют условию,  являются частотно вырожденным, хотя их пространственные конфигурации будут различными. При этом частотные интервалы между различными модами равны 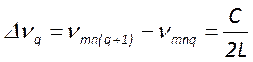; ;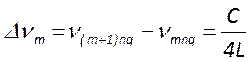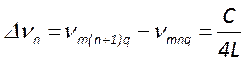, откуда следует, что все невырожденные поперечные моды расположены эквидистантно по спектру, причем расстояние между соседними модами в этом спектре равно . С другой стороны, в каждой поперечной моде соответствующие ей продольные моды также расположены эквидистантно, но с интервалом 

Билет №11

1.  Плоскопараллельный резонатор и частотный спектр его мод

Плоскопараллельный – резонатор образованный параллельными плоскими зеркалами. В нём достигается максимальная расходимость пучка по сравнению с другими видами, но наиболее часто он применяется в  тех типах лазеров, которые обладают малой длиной и достаточно хорошим  усилением активной среды, что облегчает его юстировку, поэтому наиболее широко эта конфигурация применяется в твердотельных и полупроводниковых лазерах.

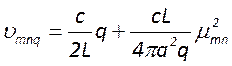Частотный спектр собственных колебаний  плоскопараллельного резонатора с круглыми зеркалами радиуса определяется формулой . Сопоставляя её с общей формулой для резонансных частот 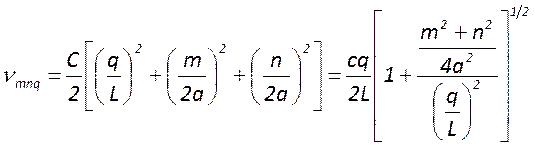, можно сделать вывод, что при имеет место полное совпадение поперечных мод по частотам. В этом случае моды называют частотно вырожденными. При этом можно считать, что в рамках некоторого приближения все поперечные моды плоскопараллельного резонатора частотно вырождены. В этом случае спектр его излучении состоит только из ряда линий, отстоящих друг от друга на частотном расстоянии