Назначение лазерного резонатора, виды потерь в лазерном резонаторе. Число Френеля и его физический смысл. Добротность лазерного резонатора и её связь с потерями в резонаторе. Добротность резонатора и её связь с полосой пропускания, страница 8

Плоскопараллельный – резонатор образованный параллельными плоскими зеркалами. В нём достигается максимальная расходимость пучка по сравнению с другими видами, но наиболее часто он применяется в  тех типах лазеров, которые обладают малой длиной и достаточно хорошим  усилением активной среды, что облегчает его юстировку, поэтому наиболее широко эта конфигурация применяется в твердотельных и полупроводниковых лазерах.

Частотный спектр собственных колебаний  плоскопараллельного резонатора с круглыми зеркалами радиуса определяется формулой 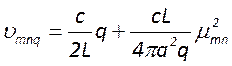. Сопоставляя её с общей формулой для резонансных частот 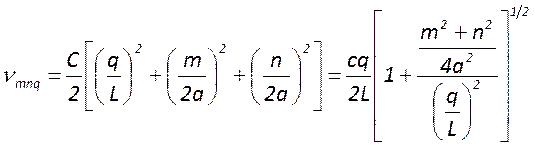, можно сделать вывод, что при имеет место полное совпадение поперечных мод по частотам. В этом случае моды называют частотно вырожденными. При этом можно считать, что в рамках некоторого приближения все поперечные моды плоскопараллельного резонатора частотно вырождены. В этом случае спектр его излучении состоит только из ряда линий, отстоящих друг от друга на частотном расстоянии

2.  Типы лазерных резонаторов

Известно, что свойства лазерных пучков почти полностью определяются геометрией резонатора. Поэтому создана классификация резонаторов по типам на основе их конфигурации. Принято считать, что каждой конфигурации соответствует свой, вполне определенный тип резонатора. В случае круглых зеркал конфигурацию можно полностью задать с помощью всего 5 параметров –

- радиусы зеркал, - радиусы их кривизны, - длина резонатора. На практике геометрические размеры резонатора задаются не в явном виде, а в виде некоторых комбинаций, имеющих определенный физический смысл. Чаще всего используют обобщенные параметры резонатора 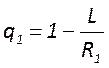,  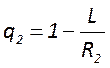которые определяют модовый состав и устойчивость. Другой комбинацией геометрических размеров являются числа Френеля 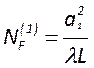, 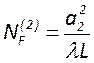и их циклические аналоги и определяющие дифракционные потери излучения.

В таблице приведены конфигурации наиболее известных типов резонаторов и их названия.

Наиболее распространены 3 конфигурации – плоскопараллельная, конфокальная и концентрическая. Для плоскопараллельной конфигурации и она всегда симметрична. Для конфокальной и она образуется совмещением фокусов зеркал. Если одно из зеркал, например, второе, является выпуклым, то условие конфокальности принимает вид   и общий фокус выносится за пределы резонатора, который тогда называется телескопическим. При конфокальный резонатор становится симметричным. Если одно из зеркал заменить на плоское и поместить его  фокусе другого, то такой резонатор будет называться полуконфокальным. При совмещении центров кривизны зеркал выполняется условие и резонатор становится концентрическим. При  концентрический резонатор превращается в симметричный и называется сферическим, так как  в этом случае поверхности его зеркал лежат на одной и той же сфере радиуса. Все другие конфигурации следует считать произвольными

Билет № 14

1.  Конфокальный резонатор и частотный спектр его мод

Конфокальным называется резонатор образованный совмещением фокусов двух изогнутых зеркал. Особенностью его является то, что поверхности  зеркал являются поверхностями равных фаз, т.е. распределение фазы по поверхности каждого зеркала резонатора. Поле в конфокальном резонаторе сконцентрировано вблизи оси. Важным является то обстоятельство, что потери мощности в таких резонаторах могут быть на несколько порядков меньше чем в плоскопараллельных.

В случае сферических зеркал с квадратной апертурой выражение для собственных частот резонатора принимает простой вид 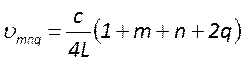. Отсюда следует, что поперечные моды, индексы которых удовлетворяют условию,  являются частотно вырожденным, хотя их пространственные конфигурации будут различными. При этом частотные интервалы между различными модами равны 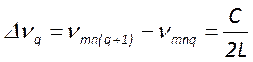; ;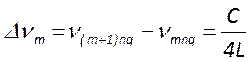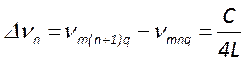, откуда следует, что все невырожденные поперечные моды расположены эквидистантно по спектру, причем расстояние между соседними модами в этом спектре равно . С другой стороны, в каждой поперечной моде соответствующие ей продольные моды также расположены эквидистантно, но с интервалом 

2.  Добротность лазерного резонатора и её связь с потерями в резонаторе

Универсальным параметром, характеризующим накопительные свойства резонатора, является его добротность. Она определяется как величина, обратно пропорциональная скорости уменьшения энергии поля в резонаторе. Аналитически её выражают в виде отношения запасенной в резонаторе энергии к энергии, теряемой им за один период колебаний Т.

.

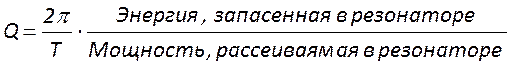Воспользуемся этим выражением и получим конкретные формулы для добротности резонатора лазера.

Пусть в резонаторе объемом имеет место собственное колебание на частоте . Пусть в начальный момент времени  в этой моде запасена энергия поля , где  - начальная объемная плотность этой энергии. При распространении от зеркала к зеркалу вдоль оси резонатора  данная мода испытывает потери своей энергии.  Обозначив суммарные потери коэффициентом 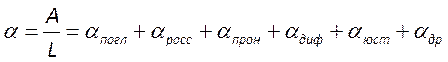, приведем уравнение баланса энергии 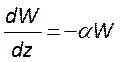к следующему виду

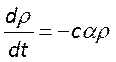. Интегрированием этого уравнения получим его решение в ви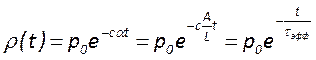де

, где .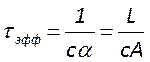

Это решение свидетельствуем об экспоненциальном характере затухания моды резонатора с характерным временем  - временем жизни фотона в моде.

Теперь легко получить выражение для добротности резонатора на частоте его моды . Действительно, если запасенная в начальные момент энергия равна , а её убыль за один период колебаний составляет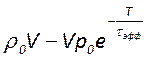, то получим

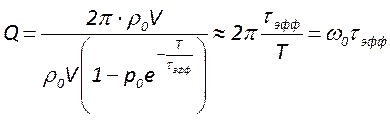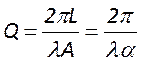; . Отсюда следует, что чем больше потери резонатора, тем меньше его добротность.

Билет №15

1.  Конфокальный резонатор и пространственные характеристики его мод

Конфокальным называется резонатор образованный совмещением фокусов двух изогнутых зеркал. Особенностью его является то, что поверхности  зеркал являются поверхностями равных фаз, т.е. распределение фазы по поверхности каждого зеркала резонатора. Поле в конфокальном резонаторе сконцентрировано вблизи оси. Важным является то обстоятельство, что потери мощности в таких резонаторах могут быть на несколько порядков меньше чем в плоскопараллельных.

Общее выражение, которое описывает  нормированное распределение интенсивности в пятне для данной моды имеет следующий вид: