Назначение лазерного резонатора, виды потерь в лазерном резонаторе. Число Френеля и его физический смысл. Добротность лазерного резонатора и её связь с потерями в резонаторе. Добротность резонатора и её связь с полосой пропускания, страница 3

2.  Неустойчивый телескопический конфокальный резонатор, его особенности и свойства

К неустойчивым относят резонаторы, для которых не выполняется условие устойчивости , где 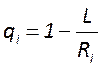- обобщенные параметры резонатора. Телескопический конфокальный резонатор состоит из двух металлических зеркал, одно из которых – вогнутое с радиусом , а второе выпуклое с радиусом . Конфокальность такого резонатора имеет место при выполнении условия .

В лазере с неустойчивым резонатором генерация возникает в приосевой зоне. Многократно отражаясь  от зеркал, излучение усиливается и покидает приосевую зону, смещаясь к периферии. Относительная величина смещения луча на выпуклом зеркале за один проход резонатора называется коэффициентом увеличение резонатора. .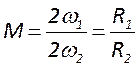

В отличие от устойчивого резонатора прозрачность неустойчивого определяется отношением площади кольца выходного излучения к площади сечения, занятого излучением:

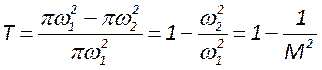
Из-за геометрического расширения в резонаторе его интенсивность на одном проходе падает в  раз. Однако в стационарных условиях генерации и при малых внутренних потерях усиление излучения на одном проходе также равно . Таким образом, весь резонатор заполнен излучением с практически равно интенсивностью, что и обеспечивает полное и равномерное использование всей активной среды, и каустика пучка имеет вид прямой линии.

Поскольку дифракционные потери в зоне зарождения генерации весьма заметны, лазеры с телескопическим конфокальным параметром работают, как правило, в одномодовом режиме .

При использовании таких резонаторов в конструкции лазера должны быть выполнены условия, в основном, определяемые свойствами и размерами активных сред. Если активная среда имеет цилиндрическую форму с длиной и радиусом , то предпосылкой для применения телескопического конфок. резонатора является выполнение условия . При этом длина резонатора определяется из условия. 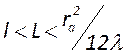, а радиусы кривизны зеркал и из апертуры по формулам 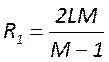;; ; 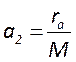. В этом случае суммарные потери (дифракционные и геометрические)

Билет №5

1.  Добротность резонатора и её связь с полосой пропускания.

Универсальным параметром, характеризующим накопительные свойства резонатора, является его добротность. Она определяется как величина, обратно пропорциональная скорости уменьшения энергии поля в резонаторе. Аналитически её выражают в виде отношения запасенной в резонаторе энергии к энергии, теряемой им за один период колебаний Т..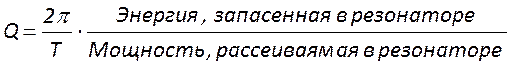

Воспользуемся этим выражением и получим конкретные формулы для добротности резонатора лазера.

Пусть в резонаторе объемом имеет место собственное колебание на частоте . Пусть в начальный момент времени  в этой моде запасена энергия поля , где  - начальная объемная плотность этой энергии. При распространении от зеркала к зеркалу вдоль оси резонатора  данная мода испытывает потери своей энергии.  Обозначив суммарные потери коэффициентом 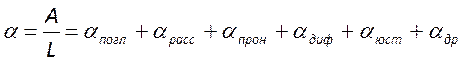, приведем уравнение баланса энергии 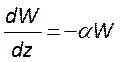 к следующему виду 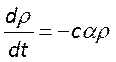.Перепишем ур-е баланса энергии резонат. так чтобы в нём в явном виде содержалась добротность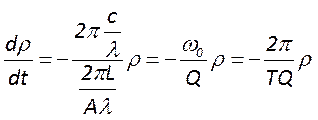

Легко видеть, что решение этого уравнения имеет вид 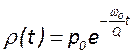. Домножая обе части на объем резонатора , получаем выражение для затухания энергии во времени .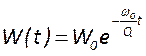

Так как нам известно, изменение энергии резонатора во времени, можно получить выражение для изменения во времени напряженности его поля: 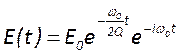. Используя преобразование Фурье можно записать 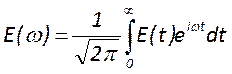.Функция представляет собой спектральное разложение внутрирезонаторного поля. Вычислим эту функцию, подставив в неё выр-е для

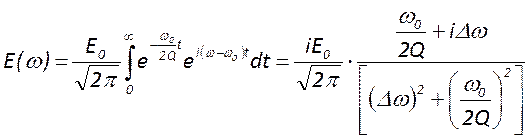, где

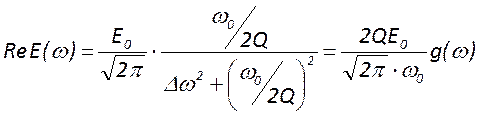- амплитуда

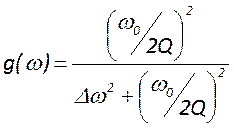- закон изменения амплитуды при изменении частоты. График его имеет вид нормированной кривой (рисунок) и лоренцеву форму. Ширина это линий, определенная на полувысоте равна 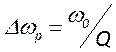 и называется полосой пропускания резонатора.

Таким образом, чем выше добротность резонатора, чем ниже его потери, тем меньше ширина соответствующей резонансной кривой и тем выше амплитуда поля соответствующей моды. Определение полосы пропускания позволяет получить формулу для нахождения добротности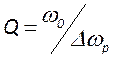

2.  Гауссов пучок и его характеристики

Гауссовым называется такой лазерный пучок, который описывается функцией Гаусса. К таким пучкам относятся все, работающие на основной моде. Их особенностью является то, что гауссов пучок преобразуется идеальной тонкой линзой в гауссов же пучок, но с другими параметрами.

Описываются же гауссовы пучки следующими параметрами

Распределение поля гауссова  пучка описывается формулой

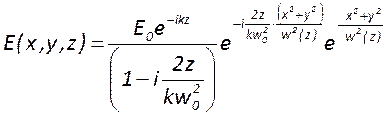
А распределение интенсивности – формулой

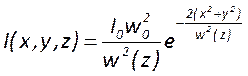, где , и значения соответствующих  величин в точке , а - значение в плоскости . Проведем в некоторой точке  плоскость, перпендикулярную оси пучка. Тогда - радиус пятна пучка в этой плоскости. На расстоянии  от оси пучка напряженность падает в а интенсивность в раз. Поверхность одинаковых значений интенсивности, проведенная на расстоянии  от пучка, называется каустикой пучка и для гауссова пучка имеет форму поверхности однополосного гиперболоида вращения. Наиболее узкий участок каустики называется её перетяжкой, а - радиусом перетяжки. Для описания гауссовых пучков также вводят параметр 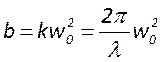 - конфокальный параметр. Он определяется как высота гиперболоида, площадь торцов которого в 2 раза больше площади его перетяжки.  Другие характеристики, определяемые для всех видов пучков – радиус кривизны волнового фронта 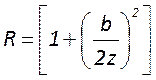и расходимость луча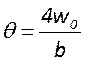

Билет №6

1.  Типы лазерных резонаторов

Известно, что свойства лазерных пучков почти полностью определяются геометрией резонатора. Поэтому создана классификация резонаторов по типам на основе их конфигурации. Принято считать, что каждой конфигурации соответствует свой, вполне определенный тип резонатора. В случае круглых зеркал конфигурацию можно полностью задать с помощью всего 5 параметров –

- радиусы зеркал, - радиусы их кривизны, - длина резонатора. На практике геометрические размеры резонатора задаются не в явном виде, а в виде некоторых комбинаций, имеющих определенный физический смысл. Чаще всего используют обобщенные параметры резонатора 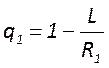,  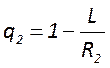которые определяют модовый состав и устойчивость. Другой комбинацией геометрических размеров являются числа Френеля 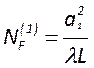, 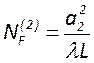и их циклические аналоги и определяющие дифракционные потери излучения.