Назначение лазерного резонатора, виды потерь в лазерном резонаторе. Число Френеля и его физический смысл. Добротность лазерного резонатора и её связь с потерями в резонаторе. Добротность резонатора и её связь с полосой пропускания, страница 10

Перепишем уравнение баланса энергии резонатора так, чтобы в нём в явном виде содержалась добротность

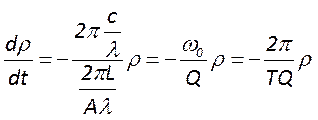                            (1)

Легко видеть, что решение этого уравнения имеет вид 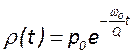. Домножая обе части на объем резонатора , получаем выражение для затухания энергии во времени

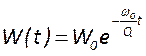. Аналогично решая уравнение баланса интенсивности, получим выражение для её затухания в пространстве .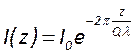

Отсюда следует, что коэффициенты затухания энергии и интенсивности обратно пропорциональны величине добротности.

2.  Типы лазерных резонаторов

Известно, что свойства лазерных пучков почти полностью определяются геометрией резонатора. Поэтому создана классификация резонаторов по типам на основе их конфигурации. Принято считать, что каждой конфигурации соответствует свой, вполне определенный тип резонатора. В случае круглых зеркал конфигурацию можно полностью задать с помощью всего 5 параметров –

- радиусы зеркал, - радиусы их кривизны, - длина резонатора. На практике геометрические размеры резонатора задаются не в явном виде, а в виде некоторых комбинаций, имеющих определенный физический смысл. Чаще всего используют обобщенные параметры резонатора 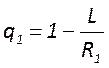,  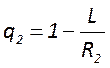которые определяют модовый состав и устойчивость. Другой комбинацией геометрических размеров являются числа Френеля 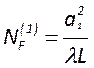, 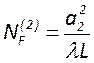и их циклические аналоги и определяющие дифракционные потери излучения.

В таблице приведены конфигурации наиболее известных типов резонаторов и их названия.

Наиболее распространены 3 конфигурации – плоскопараллельная, конфокальная и концентрическая. Для плоскопараллельной конфигурации и она всегда симметрична. Для конфокальной и она образуется совмещением фокусов зеркал. Если одно из зеркал, например второе, является выпуклым, то условие конфокальности принимает вид   и общий фокус выносится за пределы резонатора, который тогда называется телескопическим. При конфокальный резонатор становится симметричным. Если одно из зеркал заменить на плоское и поместить его  фокусе другого, то такой резонатор будет называться полуконфокальным. При совмещении центров кривизны зеркал выполняется условие и резонатор становится концентрическим. При  концентрический резонатор превращается в симметричный и называется сферическим, так как  в этом случае поверхности его зеркал лежат на одной и той же сфере радиуса. Все другие конфигурации следует считать произвольными

Билет №17

1.  Неустойчивый телескопический конфокальный резонатор, его особенности и свойства

К неустойчивым относят резонаторы, для которых не выполняется условие устойчивости , где 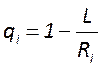- обобщенные параметры резонатора. Телескопический конфокальный резонатор состоит из двух металлических зеркал, одно из которых – вогнутое с радиусом , а второе выпуклое с радиусом . Конфокальность такого резонатора имеет место при выполнении условия .

В лазере с неустойчивым резонатором генерация возникает в приосевой зоне. Многократно отражаясь  от зеркал, излучение усиливается и покидает приосевую зону, смещаясь к периферии. Относительная величина смещения луча на выпуклом зеркале за один проход резонатора называется коэффициентом увеличение резонатора. .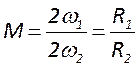

В отличие от устойчивого резонатора прозрачность неустойчивого определяется отношением площади кольца выходного излучения к площади сечения, занятого излучением:

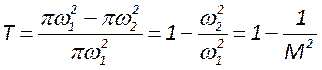
Из-за геометрического расширения в резонаторе его интенсивность на одном проходе падает в  раз. Однако в стационарных условиях генерации и при малых внутренних потерях усиление излучения на одном проходе также равно . Таким образом, весь резонатор заполнен излучением с практически равно интенсивностью, что и обеспечивает полное и равномерное использование всей активной среды, и каустика пучка имеет вид прямой линии.

Поскольку дифракционные потери в зоне зарождения генерации весьма заметны, лазеры с телескопическим конфокальным параметром работают, как правило, в одномодовом режиме .

При использовании таких резонаторов в конструкции лазера должны быть выполнены условия, в основном, определяемые свойствами и размерами активных сред. Если активная среда имеет цилиндрическую форму с длиной и радиусом , то предпосылкой для применения телескопического конфок. резонатора является выполнение условия . При этом длина резонатора определяется из условия. 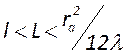, а радиусы кривизны зеркал и из апертуры по формулам 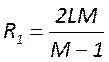;; ; 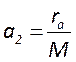. В этом случае суммарные потери (дифракционные и геометрические)

2.  Формирование стоячих волн в резонаторе. Моды резонатора

Рассмотрим условие, при котором в резонаторе возможно формирование стоячей волны.

Как известно в бегущей волне векторы и совпадает по фазе, причем для нее, всегда выполняется правило правого винта , где - вектор скорости волны. Представим изменение амплитуд векторов полей это волны в виде ; . Пусть эта волна распространяется внутри резонатора таким образом, что вектор её скорости совпадает с осью . Поскольку показатель преломления отражающих поверхностей  зеркал всегда больше показателя преломления граничащей с ним внутрирезонаторной среды, то, как известно при отражении от таких поверхностей вектор  меняет фазу на ,  а вектор  не меняет совсем. Тогда чтобы выполнялось правило правого винта, эти вектора при отражении от зеркал должны быть направлены так, как показано на рисунке.

Таким образом, внутри резонатора поле в каждой точке определяется суммой прямой и обратной волн . Преобразование этих выражений приводит к следующим формулам: ,

Известно, что интенсивность электромагнитной волны определяется вектором Умова-Пойнтинга: 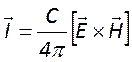. Подставляя сюда найденные выражения, получим абсолютную величину этой интенсивности: 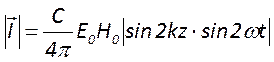. Нетрудно видеть, что данная формула описывает стоячую волну. Действительно, в точках 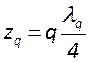интенсивность рассматриваемой волны обращается в ноль, а между ними она принимает ненулевые значения. Это означает что вся ось резонатора поделена на отрезки длиной , в которых и сосредоточена энергия волны, причем ввиду фиксированности эта энергия не может распространяться, она как бы локализована в пространстве этих отрезков, что характерно только для стоячей волны.