Назначение лазерного резонатора, виды потерь в лазерном резонаторе. Число Френеля и его физический смысл. Добротность лазерного резонатора и её связь с потерями в резонаторе. Добротность резонатора и её связь с полосой пропускания, страница 7

2.  Число Френеля и его физический смысл

Пусть в плоскопараллельном резонаторе световая волна, отраженная от первого зеркала, дифрагирует в угол, который называется дифракционным и имеет величину

Чем меньше этот угол по сравнению с углом поля зрения  - углом, под которым второе зеркало видно из центра первого, тем  эффективнее второе зеркало получает излучение, тем меньше буду потери за счет дифракции. Угол поля зрения можно выразить как 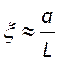, если . Тогда для уменьшения дифракц. потерь  требуется выполнение условия или 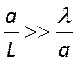. Запишем это условие в несколько ином виде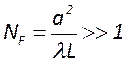

Безразмерная величина называется числом Френеля, которое является важным физическим параметром резонатора и определяет многие его свойства.  Чтобы выяснить его физический смысл, проведем разбиение отражающей поверхности  второго зеркала на зоны Френеля, которые наблюдаются из центра первого зеркала (разбиение)

Важным свойством зон Френеля является то, что они примерно равны по площади. Действительно, площадь центрального круга

А площадь первого кольца

Вообще площадь n-го кольца

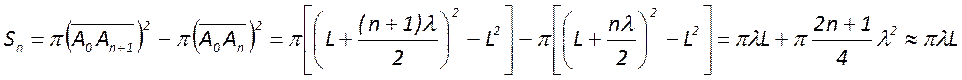Отсюда следует, что равенство площадей будет выполняться, пока выполняется условие

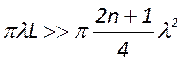или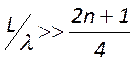

Вычислим полное число зон Френеля, умещающихся на поверхности второго зеркала

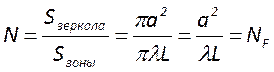. Отсюда следует, что физический смысл числа Френеля состоит в том, что оно есть число зон Френеля, наблюдаемых на поверхности одного зеркала конечной апертуры из центра другого зеркала. Однако применительно к лазерной физике его стоит трактовать по-другому. Изначально мы определили число Френеля как отношения угла поля зрения к углу дифракции. Смысл этого отношения в том, что оно будет определять  наибольшее число проходов излучения через активную среду лазера, т. е число актов усиления.

Билет №12

1.  Частотный спектр лазерного излучения и его описание

Частотный интервал между соседними продольными модами, принадлежащими одной поперечной во много раз больше интервала между двумя соседними поперечными. Действительно, интервал между соседними продольными модами

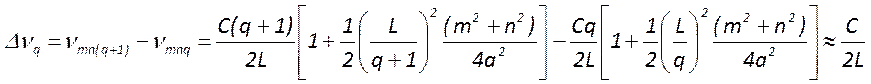, а между соседними поперечными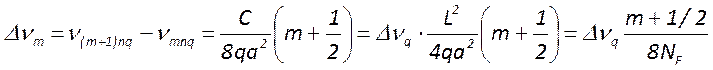

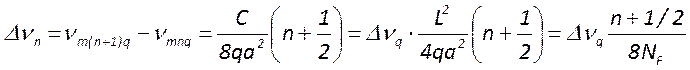
Здесь - число Френеля. Отсюда следует что ;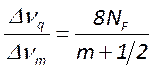

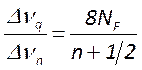
Поскольку для наиболее часто используемых резонаторов , а и имеют величину порядка нескольких единиц, то следует, что .

Для того чтобы определить, сколько резонансных частот будет присутствовать в выходном излучении лазера, необходимо знать ширину контура линии люминесценции рабочего перехода активной среды, так как именно этот диапазон определяет тот спектральный диапазон, в пределах которого осуществляется лазерная генерация. В большинстве случаев выполняется условие и в спектре излучения наблюдается много мод.

На рисунке представлена качественная картина частотного спектра лазерного излучении при использовании плоскопараллельного резонатора.  При этом следует помнить, что спектральные линии излучения, соответствующие модам, будут располагаться по всей ширине линии люминесценции, только если уровень накачки обеспечивает условие  генерации по всему контуру усиления. Если же усиление больше потерь только в определенной области контура, то спектр излучения будет наблюдаться только в этой области.

2.  Устойчивость работы резонаторов. Условие устойчивости и его анализ

Резонатор называется устойчивым, если при многократных проходах излучения между зеркалами электромагнитное поле имеет стационарный характер, а его распределение воспроизводится идентично. Это означает, что излучение не выходит за пределы зеркал в поперечном направлении и выводится только благодаря частичному пропусканию зеркал. Поэтому в устойчивом резонаторе, в случае отсутствие потерь, излучение могло бы существовать бесконечно долго. В неустойчивом резонаторе световые пучки в результате последовательных отражений от зеркал  перемещаются в поперечном направлении от оси резонатора к его периферии и покидают его.

Условие устойчивости работы резонатора может быть записано в виде, где 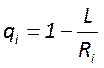- обобщенные параметры резонатора. На рисунке это условие представлено в графическом виде в q-координатах, что позволило наглядно представить область устойчивой и неустойчиво работы резонатора. График позволяет дать обобщенный анализ устойчивости работы резонаторов всех типов. Для этого обычно проводят биссектрису углов 1 и 3 четвертей координатной плоскости и рассматривают те типы резонаторов, параметры которых соответствуют точкам, лежащим на этой биссектрисе. Так как для точек на ней справедливо выполнение равенства , из которого следует равенство , то соответствующие резонаторы называются симметричными. При анализе графика можно сделать следующие выводы

7.  В области отрезка диаметр кривизны зеркал резонатора всегда меньше его длины , поэтому такой тип резонатора всегда будет неустойчивым, так как излучение быстро покидает внутрирезонаторную область через открытую боковую поверхность.

8.  В точке диаметр кривизны поверхности равен длине резонатора . Здесь резонатор становится устойчивым концентрическим

9.  В точке 0 мы имеем устойчивый симметричный конфокальный резонатор

10.  В точке зеркала становятся  плоскими, что соответствует устойчивому плоскопараллельному резонатору.

11.  Точки, лежащие на отрезке , соответствуют симметричным резонаторам с выпуклыми зеркалами, так как в этой области что соответствует . Это область неустойчивой работы, так как излучение быстро покидает внутрирезонаторную область через открытую боковую поверхность.

12.  Для несимметричных резонаторов и соответствующие им точки лежат вне биссектрисы. При этом каждому несимметричному резонатору соответствуют две точки, которые расположенные симметрично относительно биссектрисы, и которые переходят друг в друга при перестановке зеркал. Например, точки соответствуют полуконфокальным резонаторам, а точки - полуконцентрическим

Таким образом, за исключением конфокального телескопического резонатора все основные типы конфигураций относятся к устойчивым резонаторам.

Билет №13

1.  Плоскопараллельный резонатор и частотный спектр его мод