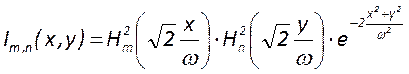 , где
, где ![]() -
параметр, характеризующий масштаб распределения;
-
параметр, характеризующий масштаб распределения; ![]() и
и ![]() - полиномы Эрмита порядка,
соответствующего индексу поперечной моды. Для типов колебаний низших порядков
полиномы Эрмита равны:
- полиномы Эрмита порядка,
соответствующего индексу поперечной моды. Для типов колебаний низших порядков
полиномы Эрмита равны: ![]() ;
;![]() ;
;
![]() ;
; ![]() .
Распределение интенсивности излучения, соответствующее низшим модам, показано
на рисунке1. Основная мода
.
Распределение интенсивности излучения, соответствующее низшим модам, показано
на рисунке1. Основная мода ![]() имеет
распределение, описываемое функцией Гаусса, симметрично расположенной
относительной начала координат. Для последующих мод характерно более сложное
распределение с симметричным чередованием максимумов и нулевых минимумов. Число
минимум в распределении равно соответствующему индексу моды, а число максимумов
– на единицу больше. Периферийные максимумы распределения больше центральных.
Иной вид имеет распределение интенсивности при центральной симметрии сечения
резонатора:
имеет
распределение, описываемое функцией Гаусса, симметрично расположенной
относительной начала координат. Для последующих мод характерно более сложное
распределение с симметричным чередованием максимумов и нулевых минимумов. Число
минимум в распределении равно соответствующему индексу моды, а число максимумов
– на единицу больше. Периферийные максимумы распределения больше центральных.
Иной вид имеет распределение интенсивности при центральной симметрии сечения
резонатора: 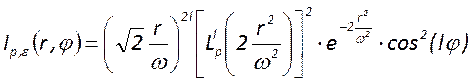 ,
,
Где ![]() - полиномы Лагерра;
- полиномы Лагерра; ![]() и
и ![]() -
соответственно радиальный и угловой индексы моды. Для типов колебаний низших
радиальных порядков полиномы Лагерра равны:
-
соответственно радиальный и угловой индексы моды. Для типов колебаний низших
радиальных порядков полиномы Лагерра равны: ![]() ;
;![]() ;
; 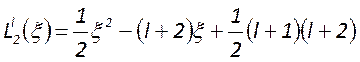 ;
;
Нетрудно заметить, что распределение в основной моде при центральной симметрии резонатора также описывается функцией Гаусса и не отличается от случая прямоугольной симметрии. Однако для типов колебания высших порядков имеет более сложный характер распределения с периодическим чередованием экстремумов.
Масштаб
распределения определяется параметром ![]() .
Величина его равна расстоянию от оси пучка до точки, где интенсивность
излучения уменьшается в
.
Величина его равна расстоянию от оси пучка до точки, где интенсивность
излучения уменьшается в ![]() раз. Этот параметр
называется размером пятна, и он зависит от конфигурации резонатора и от
координаты оси резонатора, где он измеряется.
раз. Этот параметр
называется размером пятна, и он зависит от конфигурации резонатора и от
координаты оси резонатора, где он измеряется.
Пучок имеет
сечение, в котором его размер принимает минимальное значение – перетяжку. В
резонаторе с одинаковыми зеркалами её положение совпадает с центральным
сечением. Если зеркала имеют различную кривизну, то перетяжка отстоит от
центрального сечения на некоторое расстояние, которое можно рассчитать по
формуле 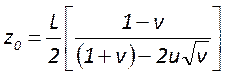 , где
, где ![]() ,
,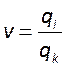 - параметры конфигурации резонатора.
В общем случае перетяжка смещена от центрального сечения в сторону зеркала
меньше кривизны. Размер её определяется параметрами конфигурации резонатора и
длиной волны излучения генерации лазера
- параметры конфигурации резонатора.
В общем случае перетяжка смещена от центрального сечения в сторону зеркала
меньше кривизны. Размер её определяется параметрами конфигурации резонатора и
длиной волны излучения генерации лазера 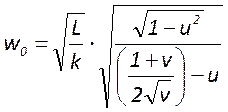 .
Размер пятна по обе стороны от перетяжки увеличивается по закону
.
Размер пятна по обе стороны от перетяжки увеличивается по закону 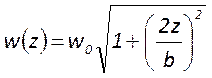 , где
, где ![]() -
конфокальный параметр резонатора.
-
конфокальный параметр резонатора.
Поверхность
равной относительной интенсивности излучения представляет собой поверхность
гиперболоида вращения, ось которого совпадает с осью резонатора. Линии,
образующиеся при осевом сечении этой поверхности плоскостью, называются
каустикой пучка. Конфокальный параметр резонатора тогда определяется как высота
гиперболоида, поверхность которого образована каустикой пучка, а площадь торцов
больше площади сечения перетяжки в два раза. На торцах такого гиперболоида
сферический волновой фронт имеет максимальную кривизну, а при удалении от них в
обе стороны уменьшается и становится плоским. Изменение радиуса кривизны
волнового фронта описывается формулой 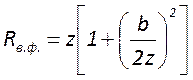
Так как
размер пятна в области ![]() растет линейно с
увеличением
растет линейно с
увеличением ![]() , это позволяет ввести еще один
параметр пучка – угол его расходимости. Его можно определить как угол, под
которым асимптота каустики наклонена к оси резонатора, и записать как
, это позволяет ввести еще один
параметр пучка – угол его расходимости. Его можно определить как угол, под
которым асимптота каустики наклонена к оси резонатора, и записать как 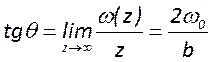 .
.
2. Добротность резонатора и её связь с полосой пропускания.
Универсальным параметром, характеризующим накопительные свойства
резонатора, является его добротность. Она определяется как величина, обратно
пропорциональная скорости уменьшения энергии поля в резонаторе. Аналитически её
выражают в виде отношения запасенной в резонаторе энергии к энергии, теряемой
им за один период колебаний Т.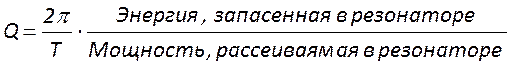 .
.
Воспользуемся этим выражением и получим конкретные формулы для добротности резонатора лазера.
Пусть в резонаторе объемом ![]() имеет место
собственное колебание на частоте
имеет место
собственное колебание на частоте ![]() . Пусть в
начальный момент времени
. Пусть в
начальный момент времени ![]() в этой моде
запасена энергия поля
в этой моде
запасена энергия поля ![]() , где
, где ![]() - начальная объемная плотность этой
энергии. При распространении от зеркала к зеркалу вдоль оси резонатора данная
мода испытывает потери своей энергии. Обозначив суммарные потери коэффициентом
- начальная объемная плотность этой
энергии. При распространении от зеркала к зеркалу вдоль оси резонатора данная
мода испытывает потери своей энергии. Обозначив суммарные потери коэффициентом
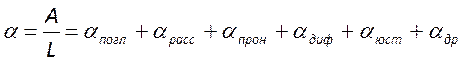 , приведем уравнение баланса энергии
, приведем уравнение баланса энергии 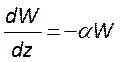 к следующему виду
к следующему виду 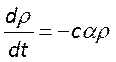 .Перепишем ур-е баланса энергии
резонат. так чтобы в нём в явном виде содержалась добротность
.Перепишем ур-е баланса энергии
резонат. так чтобы в нём в явном виде содержалась добротность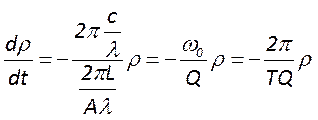
Легко видеть, что решение этого уравнения имеет вид 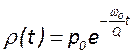 . Домножая обе части на объем
резонатора
. Домножая обе части на объем
резонатора ![]() , получаем выражение для затухания
энергии во времени
, получаем выражение для затухания
энергии во времени 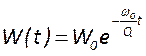 .
.
Так как нам известно, изменение энергии резонатора во времени, можно
получить выражение для изменения во времени напряженности его поля: 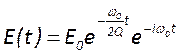 . Используя преобразование Фурье
можно записать
. Используя преобразование Фурье
можно записать 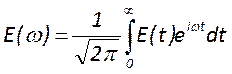 .Функция
.Функция ![]() представляет собой спектральное
разложение внутрирезонаторного поля. Вычислим эту функцию, подставив в неё
выр-е для
представляет собой спектральное
разложение внутрирезонаторного поля. Вычислим эту функцию, подставив в неё
выр-е для ![]()
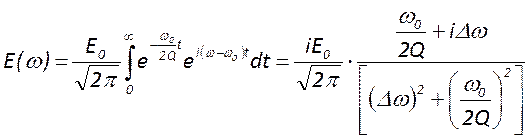 , где
, где ![]()
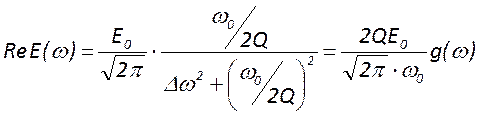 - амплитуда
- амплитуда ![]()
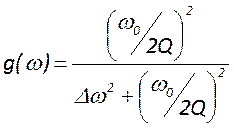 - закон изменения амплитуды при
изменении частоты. График его имеет вид нормированной кривой (рисунок) и
лоренцеву форму. Ширина это линий, определенная на полувысоте равна
- закон изменения амплитуды при
изменении частоты. График его имеет вид нормированной кривой (рисунок) и
лоренцеву форму. Ширина это линий, определенная на полувысоте равна 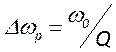 и называется полосой пропускания
резонатора.
и называется полосой пропускания
резонатора.
Таким образом, чем выше
добротность резонатора, чем ниже его потери, тем меньше ширина соответствующей
резонансной кривой и тем выше амплитуда поля соответствующей моды. Определение
полосы пропускания позволяет получить формулу для нахождения добротности 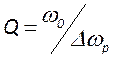
Билет №16
1. Добротность лазерного резонатора и её связь с энергией и интенсивностью излучения
Универсальным параметром, характеризующим накопительные свойства резонатора, является его добротность. Она определяется как величина, обратно пропорциональная скорости уменьшения энергии поля в резонаторе. Аналитически её выражают в виде отношения запасенной в резонаторе энергии к энергии, теряемой им за один период колебаний Т.
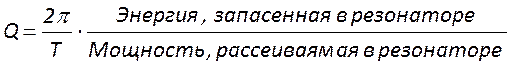 .
.
Воспользуемся этим выражением и получим конкретные формулы для добротности резонатора лазера.
Пусть в резонаторе объемом ![]() имеет место
собственное колебание на частоте
имеет место
собственное колебание на частоте ![]() . Пусть в
начальный момент времени
. Пусть в
начальный момент времени ![]() в этой моде
запасена энергия поля
в этой моде
запасена энергия поля ![]() , где
, где ![]() - начальная объемная плотность этой
энергии. При распространении от зеркала к зеркалу вдоль оси резонатора данная
мода испытывает потери своей энергии. Обозначив суммарные потери коэффициентом
- начальная объемная плотность этой
энергии. При распространении от зеркала к зеркалу вдоль оси резонатора данная
мода испытывает потери своей энергии. Обозначив суммарные потери коэффициентом
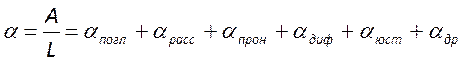 , приведем уравнение баланса энергии
, приведем уравнение баланса энергии 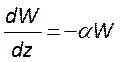 к следующему виду
к следующему виду
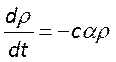
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.