Назначение лазерного резонатора, виды потерь в лазерном резонаторе. Число Френеля и его физический смысл. Добротность лазерного резонатора и её связь с потерями в резонаторе. Добротность резонатора и её связь с полосой пропускания, страница 13

Важным свойством зон Френеля является то, что они примерно равны по площади. Действительно, площадь центрального круга

А площадь первого кольца

Вообще площадь n-го кольца

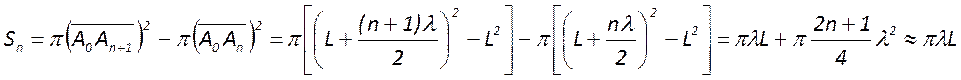Отсюда следует, что равенство площадей будет выполняться, пока выполняется условие

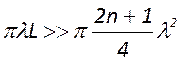или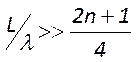

Вычислим полное число зон Френеля, умещающихся на поверхности второго зеркала

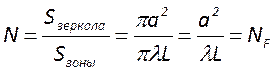. Отсюда следует, что физический смысл числа Френеля состоит в том, что оно есть число зон Френеля, наблюдаемых на поверхности одного зеркала конечной апертуры из центра другого зеркала. Однако применительно к лазерной физике его стоит трактовать по-другому. Изначально мы определили число Френеля как отношения угла поля зрения к углу дифракции. Смысл этого отношения в том, что оно будет определять  наибольшее число проходов излучения через активную среду лазера, т.е число актов усиления.

2.  Гауссов пучок и его характеристики

Гауссовым называется такой лазерный пучок, который описывается функцией Гаусса. К таким пучкам относятся все, работающие на основной моде. Их особенностью является то, что гауссов пучок преобразуется идеальной тонкой линзой в гауссов же пучок, но с другими параметрами.

Описываются же гауссовы пучки следующими параметрами

Распределение поля гауссова  пучка описывается формулой

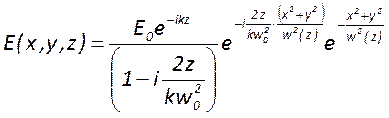
А распределение интенсивности – формулой

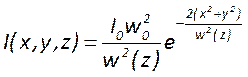, где , и значения соответствующих  величин в точке , а - значение в плоскости . Проведем в некоторой точке  плоскость, перпендикулярную оси пучка. Тогда - радиус пятна пучка в этой плоскости. На расстоянии  от оси пучка напряженность падает в а интенсивность в раз. Поверхность одинаковых значений интенсивности, проведенная на расстоянии  от пучка, называется каустикой пучка и для гауссова пучка имеет форму поверхности однополосного гиперболоида вращения. Наиболее узкий участок каустики называется её перетяжкой, а - радиусом перетяжки. Для описания гауссовых пучков также вводят параметр 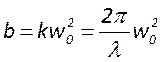 - конфокальный параметр. Он определяется как высота гиперболоида, площадь торцов которого в 2 раза больше площади его перетяжки.  Другие характеристики, определяемые для всех видов пучков – радиус кривизны волнового фронта 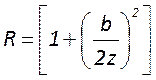и расходимость луча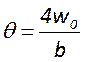

Билет №22

1.  Неустойчивый телескопический конфокальный резонатор, его особенности и свойства

К неустойчивым относят резонаторы, для которых не выполняется условие устойчивости , где 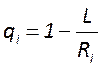- обобщенные параметры резонатора. Телескопический конфокальный резонатор состоит из двух металлических зеркал, одно из которых – вогнутое с радиусом , а второе выпуклое с радиусом . Конфокальность такого резонатора имеет место при выполнении условия .

В лазере с неустойчивым резонатором генерация возникает в приосевой зоне. Многократно отражаясь  от зеркал, излучение усиливается и покидает приосевую зону, смещаясь к периферии. Относительная величина смещения луча на выпуклом зеркале за один проход резонатора называется коэффициентом увеличение резонатора. .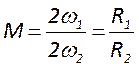

В отличие от устойчивого резонатора прозрачность неустойчивого определяется отношением площади кольца выходного излучения к площади сечения, занятого излучением:

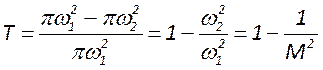
Из-за геометрического расширения в резонаторе его интенсивность на одном проходе падает в  раз. Однако в стационарных условиях генерации и при малых внутренних потерях усиление излучения на одном проходе также равно . Таким образом, весь резонатор заполнен излучением с практически равно интенсивностью, что и обеспечивает полное и равномерное использование всей активной среды, и каустика пучка имеет вид прямой линии.

Поскольку дифракционные потери в зоне зарождения генерации весьма заметны, лазеры с телескопическим конфокальным параметром работают, как правило, в одномодовом режиме .

При использовании таких резонаторов в конструкции лазера должны быть выполнены условия, в основном, определяемые свойствами и размерами активных сред. Если активная среда имеет цилиндрическую форму с длиной и радиусом , то предпосылкой для применения телескопического конфок. резонатора является выполнение условия . При этом длина резонатора определяется из условия. 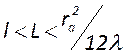, а радиусы кривизны зеркал и из апертуры по формулам 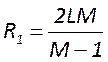;; ; 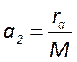. В этом случае суммарные потери (дифракционные и геометрические)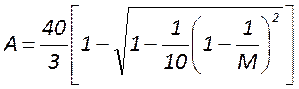

2.  Назначение лазерного резонатора, виды потерь в лазерном резонаторе

Как известно, активная среда, находясь в состоянии с инверсной населенностью, способна усиливать проходящее через неё излучение. Однако если бы излучение проходило через активную среду один раз, то мощность выходящего излучения была бы небольшой. Кроме того, оно не имело бы преимущественного направления распространения. Поэтому основным назначением резонатора лазера является создание таких условий, при которых возникающее внутри него индуцированное излучение многократно проходит через активную среду. Это достигается выбором определенного взаимного расположения зеркал резонатора (юстировкой).

Резонатор в значительной степени определяет свойства  выходного лазерного излучения. Направленность процесса усиления волн полностью зависит от конфигурации резонатора – от размера и формы его зеркал и расстояния между ними. Поэтому геометрия резонатора определяет направленность выходного излучения, угол его расходимости и вообще все пространственные характеристики лазерного пучка. Но также она определяет и частотный спектр излучения, делая лазер одномодовым, многомодовым или одночастотным. Таким образом, когерентные свойства пучка, как временные, так и пространственные, определяются в конечном итоге геометрией резонатора лазера.

              Рассмотрим плоскопараллельный резонатор, в котором расстояние между зеркалами равно. Введем в пространстве резонатора систему декартовых координат, так чтобы ее центр совпадал с центром первого зеркала, а поверхность этого зеркала лежала в плоскости . Тогда ось будет перпендикулярна обоим зеркалам и становится осью резонатора. При распространении излучения от зеркала к зеркалу оно испытывает потери энергии связанные с её поглощением, рассеянием, пропусканием зеркал, дифракцией, неточностью юстировки и пр.  Математически влияние этих потерь можно учесть в уравнении баланса