Назначение лазерного резонатора, виды потерь в лазерном резонаторе. Число Френеля и его физический смысл. Добротность лазерного резонатора и её связь с потерями в резонаторе. Добротность резонатора и её связь с полосой пропускания, страница 4

В таблице приведены конфигурации наиболее известных типов резонаторов и их названия.

Наиболее распространены 3 конфигурации – плоскопараллельная, конфокальная и концентрическая. Для плоскопараллельной конфигурации и она всегда симметрична. Для конфокальной и она образуется совмещением фокусов зеркал. Если одно из зеркал, например второе, является выпуклым, то условие конфокальности принимает вид   и общий фокус выносится за пределы резонатора, который тогда называется телескопическим. При конфокальный резонатор становится симметричным. Если одно из зеркал заменить на плоское и поместить его  фокусе другого, то такой резонатор будет называться полуконфокальным. При совмещении центров кривизны зеркал выполняется условие и резонатор становится концентрическим. При  концентрический резонатор превращается в симметричный и называется сферическим, так как  в этом случае поверхности его зеркал лежат на одной и той же сфере радиуса. Все другие конфигурации следует считать произвольными

2.  Гауссов пучок и его характеристики

Гауссовым называется такой лазерный пучок, который описывается функцией Гаусса. К таким пучкам относятся все, работающие на основной моде. Их особенностью является то, что гауссов пучок преобразуется идеальной тонкой линзой в гауссов же пучок, но с другими параметрами.

Описываются же гауссовы пучки следующими параметрами

Распределение поля гауссова  пучка описывается формулой

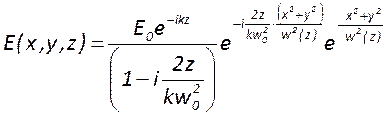
А распределение интенсивности – формулой

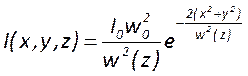, где , и значения соответствующих  величин в точке , а - значение в плоскости . Проведем в некоторой точке  плоскость, перпендикулярную оси пучка. Тогда - радиус пятна пучка в этой плоскости. На расстоянии  от оси пучка напряженность падает в а интенсивность в раз. Поверхность одинаковых значений интенсивности, проведенная на расстоянии  от пучка, называется каустикой пучка и для гауссова пучка имеет форму поверхности однополосного гиперболоида вращения. Наиболее узкий участок каустики называется её перетяжкой, а - радиусом перетяжки. Для описания гауссовых пучков также вводят параметр 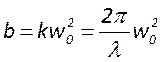 - конфокальный параметр. Он определяется как высота гиперболоида, площадь торцов которого в 2 раза больше площади его перетяжки.  Другие характеристики, определяемые для всех видов пучков – радиус кривизны волнового фронта 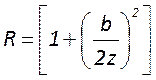и расходимость луча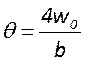

Билет №7.

1.  Устойчивость работы резонаторов. Условие устойчивости и его анализ

Резонатор называется устойчивым, если при многократных проходах излучения между зеркалами электромагнитное поле имеет стационарный характер, а его распределение воспроизводится идентично. Это означает, что излучение не выходит за пределы зеркал в поперечном направлении и выводится только благодаря частичному пропусканию зеркал. Поэтому в устойчивом резонаторе, в случае отсутствие потерь, излучение могло бы существовать бесконечно долго. В неустойчивом резонаторе световые пучки в результате последовательных отражений от зеркал  перемещаются в поперечном направлении от оси резонатора к его периферии и покидают его.

Условие устойчивости работы резонатора может быть записано в виде, где 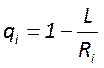- обобщенные параметры резонатора. На рисунке это условие представлено в графическом виде в q-координатах, что позволило наглядно представить область устойчивой и неустойчиво работы резонатора. График позволяет дать обобщенный анализ устойчивости работы резонаторов всех типов. Для этого обычно проводят биссектрису углов 1 и 3 четвертей координатной плоскости и рассматривают те типы резонаторов, параметры которых соответствуют точкам, лежащим на этой биссектрисе. Так как для точек на ней справедливо выполнение равенства , из которого следует равенство , то соответствующие резонаторы называются симметричными. При анализе графика можно сделать следующие выводы

1.  В области отрезка диаметр кривизны зеркал резонатора всегда меньше его длины , поэтому такой тип резонатора всегда будет неустойчивым, так как излучение быстро покидает внутрирезонаторную область через открытую боковую поверхность.

2.  В точке диаметр кривизны поверхности равен длине резонатора . Здесь резонатор становится устойчивым концентрическим

3.  В точке 0 мы имеем устойчивый симметричный конфокальный резонатор

4.  В точке зеркала становятся  плоскими, что соответствует устойчивому плоскопараллельному резонатору.

5.  Точки, лежащие на отрезке , соответствуют симметричным резонаторам с выпуклыми зеркалами, так как в этой области что соответствует . Это область неустойчивой работы, так как излучение быстро покидает внутрирезонаторную область через открытую боковую поверхность.

6.  Для несимметричных резонаторов и соответствующие им точки лежат вне биссектрисы. При этом каждому несимметричному резонатору соответствуют две точки, которые расположенные симметрично относительно биссектрисы, и которые переходят друг в друга при перестановке зеркал. Например, точки соответствуют полуконфокальным резонаторам, а точки - полуконцентрическим

Таким образом за исключением конфокального телескопического резонатора все основные типы конфигураций относятся к устойчивым резонаторам.

2.  Формирование стоячих волн в резонаторе. Моды резонатора

Рассмотрим условие, при котором в резонаторе возможно формирование стоячей волны.

Как известно в бегущей волне векторы и совпадает по фазе, причем для нее, всегда выполняется правило правого винта , где - вектор скорости волны. Представим изменение амплитуд векторов полей это волны в виде ; . Пусть эта волна распространяется внутри резонатора таким образом, что вектор её скорости совпадает с осью . Поскольку показатель преломления отражающих поверхностей  зеркал всегда больше показателя преломления граничащей с ним внутрирезонаторной среды, то, как известно при отражении от таких поверхностей вектор  меняет фазу на ,  а вектор  не меняет совсем. Тогда чтобы выполнялось правило правого винта, эти вектора при отражении от зеркал должны быть направлены так, как показано на рисунке.

Таким образом, внутри резонатора поле в каждой точке определяется суммой прямой и обратной волн . Преобразование этих выражений приводит к следующим формулам: ,