Назначение лазерного резонатора, виды потерь в лазерном резонаторе. Число Френеля и его физический смысл. Добротность лазерного резонатора и её связь с потерями в резонаторе. Добротность резонатора и её связь с полосой пропускания, страница 5

Известно, что интенсивность электромагнитной волны определяется вектором Умова-Пойнтинга: 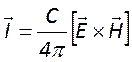. Подставляя сюда найденные выражения, получим абсолютную величину этой интенсивности: 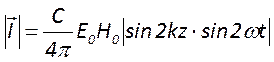. Нетрудно видеть, что данная формула описывает стоячую волну. Действительно, в точках 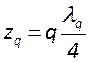интенсивность рассматриваемой волны обращается в ноль, а между ними она принимает ненулевые значения. Это означает что вся ось резонатора поделена на отрезки длиной , в которых и сосредоточена энергия волны, причем ввиду фиксированности эта энергия не может распространяться, она как бы локализована в пространстве этих отрезков, что характерно только для стоячей волны.

Моды резонатора – теперь рассмотрим пустой прямоугольный резонатор с размерами как на рисунке 1. Если он заполнен излучением то оно принимает равновесное распределение, при котором составляющие напряженности его электрического поля можно представить в виде

(1) ,, где , а- целые положительные числа. Резонансные частоты таких стоячих волн определяются формулой

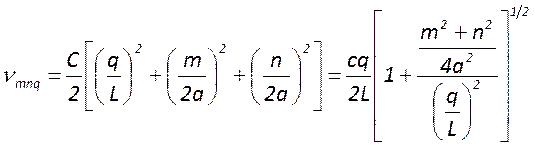. При этом для каждого набора чиселсуществует вполне определенная мода с вполне определенной резонансной частотой. Индекс равен числу полуволн укладывающихся на длине резонатора , и называется продольным индексом, а индексы и обозначают число изменений знака поля на поверхности зеркал, и называются поперечными индексами

Билет №8

1.  Подобие резонаторов. Условие подобия

Одной из задач лазерной физики является задача подбора эквивалентных резонаторов, решение которой позволяет, в частности, сводить многокомпонентные системы к простым двузеркальным. При этом под эквивалентными понимаются такие резонаторы, у которых одинаковы дифракционные потери, резонансные частоты и распределения поля на зеркалах. Такую эквивалентность часто называют подобием. Для решения этой задачи можно на основании известных свойств резонатора установить условия, которым должны удовлетворять параметры резонатора при переходе к его эквивалентному  аналогу, которые называются условиями подобия.

Первое условие подобия заключается в том, что одновременная замена и означает просто перенумерацию зеркал и не меняет свойств резонатора.

Второе условие подобия заключается в замене  при неизменности поперечных размеров резонатора и , поскольку такая замена также не меняет свойств резонатора.

Третье условие подобия формулируется следующим образом. Пусть один из резонаторов описывается тремя величинами:

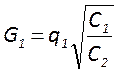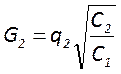;; ; и представляющими собой некоторые комбинации его геометрических размеров, а второй – аналогичными величинами

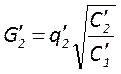;; . Тогда условие подобия рассматриваемых резонаторов имеет вид ;;

Четвертое условие подобия применимо только к тем резонаторам, у которых апертуры зеркал очень сильно различаются. Пусть у рассматриваемого резонатора выполняется условие 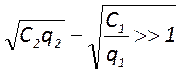. Тогда можно заменить такой произвольный резонатор на эквивалентный ему симметричный резонатор апертурный размер , длина и радиус кривизны зеркал которого определяется соотношениями 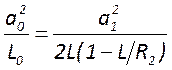; 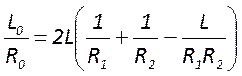. Где индекс 1 относится к зеркалу меньшего сечения, а индекс 2 – большего. При этом односторонний проход в эквивалентном симметричном резонаторе соответствует циклическому проходу  в реальном резонаторе. Средние за проход коэффициент потерь и фазовый набег в реальном резонаторе можно выразить через аналогичные параметры эквивалентного ;

Пятое условие подобия относится к тем резонаторам, у которых сечение пучка ограничено не апертурой зеркал, а какой-либо диафрагмой между ними.  Пусть симметричный резонатор длиной , составлен из одинаковых зеркал с радиусом кривизны и апертруным размером , а в центре расположена диафрагма с диаметром отверстия . Тогда вследствие симметрии схемы целесообразно рассматривать структуру, образованную диафрагмой и зеркалом как самостоятельный несимметричный резонатор длиной и обобщенным параметром . Поэтому резонатор с диафрагмой подобен обычному симметричному резонатору без диафрагмы, у которого изменяется только апертурный размер зеркал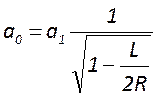

2.  Обозначение и классификация мод резонатора

 В теории открытых колебаний типы колебаний принято обозначать как (TEM – аббревиатура от Transverse Electric and Magnetic – Поперечный электрический и магнитный вектор).  Индекс m указывает на количество изменений направления поля вдоль оси x, индекс n – вдоль оси y, индекс q показывает число полуволн, которое укладывается на длине резонатора. Значения индексов выводятся из выражения для резонансной частоты моды резонатора 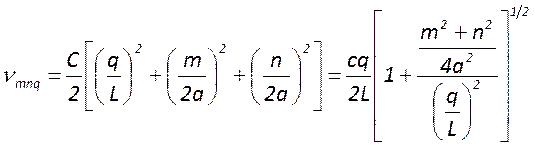.  Такая форма обозначения мод резонатора явилась основой для их классификации. Суть её такова

1.  Мода, у которой поперечные индексы (m,n) фиксированы, а продольный индекс (q) является произвольным – называется поперченной модой. Она включает в себя столько колебаний, сколько принимает значений индекс q. Обозначается она как

2.  Мода, у которой все индексы фиксированы, называется продольной (аксиальной) модой. Она имеет единственную резонансную частоту и является одной из компонент поперечной моды с теми же фиксированными m и n

3.  Поперечная мода с нулевыми поперечными индексами называется основной поперечной модой.

4.  При обозначении поперечной моды для резонатора с прямоугольными зеркалами на первое место ставится тот поперечный индекс, который соответствует большей стороне прямоугольника.

5.  Для круглых зеркал обозначение соответствует цилиндрической системе координат,  поэтому первый индекс обозначает число изменений знака поля по радиусу зеркала, а второй – по углу.

Различия между модами – см рисунок.

Билет №9

1.  Формирование стоячих волн в резонаторе. Моды резонатора

Рассмотрим условие, при котором в резонаторе возможно формирование стоячей волны.

Как известно в бегущей волне векторы и совпадает по фазе, причем для неё всегда выполняется правило правого винта , где - вектор скорости волны. Представим изменение амплитуд векторов полей это волны в виде ; . Пусть эта волна распространяется внутри резонатора таким образом, что вектор её скорости совпадает с осью . Поскольку показатель преломления отражающих поверхностей  зеркал всегда больше показателя преломления граничащей с ним внутрирезонаторной среды, то, как известно при отражении от таких поверхностей вектор  меняет фазу на ,  а вектор  не меняет совсем. Тогда чтобы выполнялось правило правого винта, эти вектора при отражении от зеркал должны быть направлены так, как показано на рисунке.