













































Ю. В. АФАНАСЬЕВ - Н.В. СТУДЕНЦОВ • А.П. ЩЕЛКИН
Магнитометрические преобразователи, приборы, установки
Ю. В. АФАНАСЬЕВ, Н. В. СТУДЕНЦОВ, А. П. ЩЕЛКИН
Магнитометрические преобразователи, приборы, установки
«ЭНЕРГИЯ» Ленинградское отделение 1972
6П2.1.08 А94
УДК 621.317.4
3-3-13
258-72
Книга посвящена теории и практике современных средств измерения магнитной индукции. Рассмотрены принцип работы, основные параметры и характеристики магнитометрических преобразователей различных типов. Дано описание схем и конструкций приборов, использующих указанные преобразователи. Уделено внимание минимизации погрешностей преобразователей и приборов, описаны методика и аппаратура для выявления частных погрешностей приборов.
Книга рассчитана на научных работников, инженеров и техников, имеющих отношение к магнитным измерениям. Она может быть полезной студентам старших курсов соответствующих вузов.
Рецензент С. Л. Спектор
Часть первая МАГНИТОМЕТРИЧЕСКИЕ
ПРЕОБРАЗОВАТЕЛИ
Глава первая ПРИНЦИПЫ ПРЕОБРАЗОВАНИЯ МАГНИТНОЙ ИНДУКЦИИ
1-1. Магнитное поле, его электрокинетическая природа
Существование магнитного поля может быть обнаружено по силе заимо действия магнита или элемента тока с исследуемым полем, а также в результате возникновения э. д. с. электромагнитной индукции в контуре, когда магнитное поле изменяется во времени или когда контур движется в этом поле [1-1—1-4].
Силовое взаимодействие и электромагнитная индукция являются фундаментальными проявлениями магнитного поля и могут быть положены в основу определения физической величины, характеризующей интенсивность или силу в каждой точке пространства. Такой величиной служит вектор магнитной индукции В.
В соответствии с законом Ампера сила, действующая на элементарный проводник длиной dl, помещенный в поле с магнитной индукцией В, равна dF = I [dl • В], где I — ток, протекающий по проводнику. Следовательно, вектор В может быть определен по силе взаимодействия элемента тока Idl с исследуемым магнитным полем.
В системе СИ величина В измеряется в теслах (в системе СГС — в гауссах; 1 гс = 10-4 тл).
Интеграл вектора магнитной индукции по некоторой поверхности
называется магнитным потоком Ф через эту поверхность:
Ф = ![]() В ds.
В ds.
Магнитный поток измеряется в веберах (в системе СГС — в максвеллах; 1 мкс — 10-8 вб) и является величиной скалярной.
Для большей наглядности часто пользуются представлением о линиях магнитной индукции. Эти линии изображают так, что касательная к ним в каждой точке совпадает по направлению с вектором магнитной индукции в той же точке. Число линий, проходящих через некоторую поверхность, характеризует значение магнитного потока. Число линий, отнесенное к единице площади, очевидно, будет характеризовать значение магнитной индукции. Другими словами, величину В можно рассматривать как плотность магнитного потока, т. е. В = Ф/s.
Если взамен элемента тока ldl использовать элемент материального контура, движущийся в поле В со скоростью v, то на каждый его свободный заряд q будет действовать сила F = q [v • В]. Такая же сила действует и на отдельную заряженную частицу, движущуюся в магнитном поле со скоростью v.
Подобно напряженности электрического поля Е вектор магнитной индукции В определяет силу, испытываемую зарядом. Произведение [v • B] можно рассматривать поэтому как одну из слагающих электрического поля Е = [v • В]. Это поле называют полем движения.
Интеграл по замкнутому контуру
в поле движения определяет значение э.д.с. электромагнитной индукции едв
= ![]() [v • B]dl, которая возникает даже в том
случае, когда поле В не зависит от времени и является однородным. Таким
образом, магнитная индукция может быть определена не только по силе
взаимодействия элемента тока с магнитным полем, но и по значению э. д. с.
электромагнитной индукции.
[v • B]dl, которая возникает даже в том
случае, когда поле В не зависит от времени и является однородным. Таким
образом, магнитная индукция может быть определена не только по силе
взаимодействия элемента тока с магнитным полем, но и по значению э. д. с.
электромагнитной индукции.
Важный вывод, следующий из только что сформулированных основных закономерностей, заключается в том, что магнитное поле проявляется в форме сил, действующих на движущиеся электрические заряды, независимо от того, движутся ли они относительно проводника или вместе с ним.
Возникновение магнитного поля связано с движением электрических зарядов. Это следует из гипотезы Ампера о молекулярных токах, объясняющей природу магнетизма, является обобщением опытных данных, в частности открытия Эрстеда (отклонение магнитной стрелки током), и формулируется в законе Био—Савара. В соответствии с этим законом элементарный вектор магнитной индукции в отсутствие намагничиваемых сред равен:
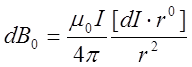 , (1-1)
, (1-1)
где ![]() =4π
=4π![]() 10-7 гн/м — магнитная постоянная, зависящая от выбранной
системы единиц; r — расстояние от элемента тока Idl до точки, где наблюдается магнитная индукция; r0 — единичный вектор, направленный
вдоль этого расстояния.
10-7 гн/м — магнитная постоянная, зависящая от выбранной
системы единиц; r — расстояние от элемента тока Idl до точки, где наблюдается магнитная индукция; r0 — единичный вектор, направленный
вдоль этого расстояния.
Значение магнитной индукции в рассматриваемой точке можно получить путем интегрирования по замкнутому контуру l выражения (1-1):
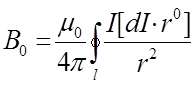
Из изложенного следует, что магнитное поле как по форме своего проявления, так и по природе является полем электрокинетическим.
Когда хотят охарактеризовать
магнитный эффект тока вне зависимости от магнитной проницаемости среды ![]() , то пользуются величиной Н = В0 /
, то пользуются величиной Н = В0 /![]() , называемой напряженностью магнитного поля. Напряженность
поля является удобной расчетной величиной и измеряется в амперах на метр (в
системе СГС — в эрстедах, э; lэ = 103/4π а/м).
, называемой напряженностью магнитного поля. Напряженность
поля является удобной расчетной величиной и измеряется в амперах на метр (в
системе СГС — в эрстедах, э; lэ = 103/4π а/м).
В отсутствие намагничиваемых сред, очевидно, нет какой-либо надобности в использовании двух векторов, так как связь между ними проста. Для описания структуры поля можно с равным правом использовать как вектор В0, так и вектор Н.
В намагничиваемых средах направления линий индукции и напряженности поля могут не совпадать. Связь между векторами задается здесь в виде:
В=[![]() ]
]![]() Н, где [
Н, где [![]() ] —тензор относительной магнитной проницаемости среды
— безразмерная величина. Тензор [
] —тензор относительной магнитной проницаемости среды
— безразмерная величина. Тензор [![]() ] учитывает анизотропные
свойства среды, т.е. неодинаковость ее магнитных свойств в различных
направлениях. В действительности связь между векторами В и Н оказывается еще более сложной.
Например, в ферромагнитных средах наблюдается двузначность (гистерезис) и
нелинейность зависимости В = f(Н),
другими
словами, компоненты тензора [
] учитывает анизотропные
свойства среды, т.е. неодинаковость ее магнитных свойств в различных
направлениях. В действительности связь между векторами В и Н оказывается еще более сложной.
Например, в ферромагнитных средах наблюдается двузначность (гистерезис) и
нелинейность зависимости В = f(Н),
другими
словами, компоненты тензора [![]() ] оказываются функциями
компонент вектора Н или В0. Очевидно, что магнитный эффект тока в намагничиваемых
средах должен характеризоваться уже не одним, а двумя векторами. Ими могут быть
векторы В и Н либо векторы В и В0.
] оказываются функциями
компонент вектора Н или В0. Очевидно, что магнитный эффект тока в намагничиваемых
средах должен характеризоваться уже не одним, а двумя векторами. Ими могут быть
векторы В и Н либо векторы В и В0.
В частном случае, когда магнитная среда изотропна [µ] = µ и В=µ µ0Н = µаH или В = µB0. Здесь, очевидно В || Н и В || В0. Произведение µ0µ = µa называют абсолютной магнитной проницаемостью среды.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.