Магнитометрические преобразователи, приборы, установки, страница 7

С этой точки зрения можно было бы, как это рекомендовал еще Максвелл [1-9], разделить измеряемые величины на скалярные, векторные и тензорные. Однако следует помнить, что непосредственно измеряемыми величинами всегда являются скаляры. Лишено какого-либо смысла деление преобразователей на скалярные, векторные и тензорные. Лишь приборы как некие совокупности измерительных средств по своей информативности могут быть разделены на скаляр и тензор-изме­рители в том смысле, что с их помощью можно обнаружить данные величины и по­компонентно измерить их.

Все существующие и потенциально возможные преобразователи могут быть объединены в три группы по функциональной связи выходного сигнала с непосредственно измеряемой величиной:

ρ=f_I(φ),φ+;

ρ=f_II(B),B=|B|;

ρ=f_III(B_i),B_i=B.

Здесь ρ — параметр выходного сигнала (механическое перемещение, электрическое напряжение, частота колебаний и т. д.); i° — некоторое заданное направление  — магнитная ось преобразователя.

Объединение различных типов преобразователей в указанные группы позволяет выработать единые критерии для оценки их метрологических, технических и эксплуатационных характеристик. Кроме того, объединение в группы позволяет широко пользоваться методом аналогий, перенося положительный опыт применения одного типа преобразователей на другой.

Часть вторая       Основные характеристики

Преобразователей

3-3. Взаимодействие с магнитным полем. Чувствительность

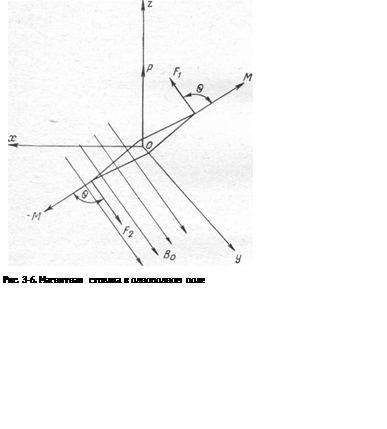
Предположим теперь, что механический преобразователь (маг­нитная стрелка) помещен в однородное поле с магнитной индук­цией В₀ (рис. 3-6). В этом случае со стороны поля на стрелку будет действовать механический вращающий момент Р=[МВ₀] (см. § 1-3) или в скалярной форме записи: Р = МВ₀ sin θ, где М — магнитный момент стрелки; θ — угол между векторами М и В₀. Момент Р урав­новешивается противодействующим моментом Р_пр : МВ₀ sin θ = Р_пр, откуда

θ = arcsin Р_пр/МВ₀.                                         (3-1)

Преобразователи первой группы стремятся выполнять таким об­разом, чтобы противодействующий момент был как можно ближе к нулю. Тогда θ ≈ 0, и направление магнитной стрелки практически совпадает с направлением В₀. Однако на практике противодействую­щий момент почти всегда имеет некоторое конечное значение, обус­ловленное наличием трения, если стрелка расположена на острие иглы, или наличием кручения, если она подвешена на нити. В этом случае угол θ также будет отличен от нуля и равен некоторому углу θ₀, значение которого определяет угловую погрешность меха­нических преобразователей, предназначенных для определения на­правления вектора В₀. Наименьшим противодействующим моментом обладают преобразователи, выполненные в виде магнитной стрелки, прикрепленной к поплавку, опущенному в жидкость.

Рассмотрим теперь условия равновесия в магнитном поле преобра­зователей второй группы:

1.  Магнитная стрелка подвешена на упругой ни­ти. При наличии кручения на нее будет действо­вать, кроме момента Р = MB₀sin θ, противодействующий мо­мент Р_пр = сφ, где φ — угол закручивания нити, а с – коэффициент кручения (удельный противодействующий момент). Так как в состоянии равновесия МВ₀sinθ=сφ, то угол φ, на который отклоняется стрелка в магнитном поле, равен φ=SB₀, где

S = .                               (3-2)

Поскольку угол φ является выходной величиной механического пре­образователя, то коэффициент S можно рассматривать как его чув­ствительность к магнитной индукции В₀. Как видно из формулы (3-2), чувствительность механического преобразователя зависит от угла θ между осью магнитной стрелки и направлением магнитной индук­ции В₀ и имеет максимальное значение при θ = 90°. Этим обстоя­тельством обычно пользуются на практике, располагая магнитную стрелку так, чтобы ее магнитная ось была перпендикулярна измеряе­мой компоненте магнитной индукции.

2. Магнитная стрелка подвешена на растянутых нитях. Пусть при этом центр тяжести расположен таким образом (рис. 3-7), что уравновешивание происходит одновременно за счет силы тяжести и момента кручения нити. В этом случае условие равновесия можно записать так: (M_xB_0z-M_zB_0x)=±сφ+Mglcos(β-θ), где B_0z, B_0x – вертикальная и горизонтальная составляющие магнит­ной индукции; М_z и М_х — составляющие магнитного момента стрелки по осям z и х; М — масса стрелки; g — ускорение свобод­ного падения; l — расстояние от центра тяжести до оси вращения стрелки.

Заменив проекции магнитного момента М_z и М_х их выраже­ниями через момент М, получим

MB_0z cos θ - МВ_0x sin θ = ±сφ + Mgl cos β cos θ - Mgl sin β sin θ.       (3-3)

Как видно из выражения (3-3), при малых значениях угла θ, т, е. когда магнит расположен горизонтально, членом, содержащим В_0x, можно пренебречь и, наоборот, когда магнит расположен верти­кально, то можно пренебречь членом, содержащим B_0z. Таким об­разом, подвешивая стрелку в вертикальном или горизонтальном положении, можно производить измерение соответственно горизонталь­ной или вертикальной составляющей магнитной индукции. Это свойство преобразователей на растянутых нитях и ножевых опорах используется при разработке приборов, получивших название маг­нитных весов (см. § 8-1).

Определим чувствительность магнитной стрелки, подвешенной вертикально или горизонтально. Для этого продифференцируем вы­ражение (3-3), считая М, с, М, g, l и β величинами постоянными, а φ = θ, и перейдем затем к конечным приращениям:

M∆B_0zcosθ – MB_0zsinθ∆θ – MB_0xsin θ – MB_0xcos θ∆ θ =

= ±c∆θ – Mglcosθsinθ – Mglsin θ cos θ

Если магнитная стрелка расположена горизонтально, так что sin θ = 0, a cos θ = 1, то

∆B_0z=()∆θ,

где z_c = lsinβ — расстояние от центра тяжести до оси магнита. Обычно при измерении вертикальной составляющей магнитной ин­дукции магнит располагают так, чтобы его магнитная ось была пер­пендикулярна В_ох. В этом случае чувствительность преобразователя к вертикальной составляющей В₀ будет:

S_z=.

Если магнитная стрелка расположена вертикально, так что ее ось перпендикулярна B0z, то, проделав те же преобразования, можно получить аналогичную формулу:

S_z=.

где х_с = l cos β.