В активных преобразователях управляемый процесс перекачки энергии сопровождается неуправляемым, приводящим к возникновению ложного выходного сигнала. Этот ложный сигнал связан либо с прямым проникновением энергии из дополнительной цепи в выходную, например за счет разбаланса схемы и несовершенства конструкции преобразователя, либо обусловлен наводками одной цепи на другую. Наличие ложного сигнала ухудшает порог чувствительности активных преобразователей.
Особую группу активных преобразователей образуют такие, в которых влияние неуправляемого процесса перекачки энергии ослаблено за счет временного или частотного разделения сигнала и помехи. При временном разделении интервалы накачки (ввода дополнительной энергии) и собственно преобразования разнесены во времени. При частотном разделении механизм преобразования таков, что сигнал и помеха характеризуются различным спектральным составом. Подобный механизм разделения действует, например, в индукционных четногармонйческих преобразователях, которые в последние годы получают все более широкое распространение.
Для того чтобы были ясны преимущества четногармонйческих преобразователей, остановимся более подробно (чем мы это сделали в § 4-1) на самом механизме преобразования. Теперь нас будет интересовать не только полезный сигнал, но и помеха (ложный сигнал), появляющаяся в результате упомянутого неуправляемого процесса.
Структурная схема активного индукционного преобразователя показана на рис. 4-7.
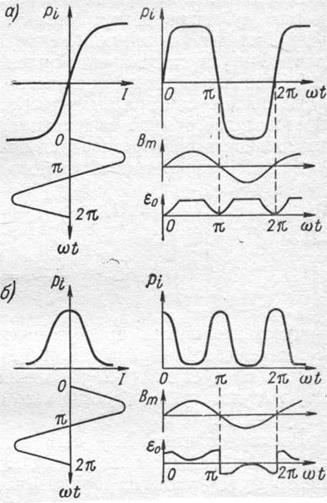
Рис. 4-8. Эпюры, поясняющие возникновение
э. д. с.-помехи на четных (а)и нечетных (б) гармониках
Здесь в верхнем прямоугольнике
записан оператор преобразования вектора В0 в э. д. с, причем единичный
вектор 
есть магнитная ось преобразователя (см. § 2-3). В
нижнем прямоугольнике записана функциональная связь параметра pш с переменным током I(t), за счет энергии которого и
осуществляется изменение параметра. Часть этой энергии проникает в выходную
цепь, образуя ложный сигнал.
Спектр выходной э. д. с. зависит от спектра pi(t). Связь рi = f (I) в общем случае нелинейна. Поэтому, если I(t) = Im sin ωt, причем Im = const и ω = const, то изменение параметра записывается в виде ряда Фурье:
pi(t)=p0+
, (4-20)
где р0 — постоянная составляющая процесса; рn и ψn — амплитуда и начальная фаза соответствующей гармоники; n = 1, 2, 3, . . . — целые числа.
Ряд (4-20) соответствует
произвольной зависимости pi = f(I). Однако различают два
частных случая (см. рис. 4-8): 1) зависимость является нечетной: f(-I) = -f(I); 2) четной: f(-I) = f(I). В первом случае (рис. 4-8, а) зависимость рi(t) 
может быть разложена в ряд:
pi
(t)
= 
p(2n-i) sin (2n-l)ωt, (4-21)
содержащий только нечетные гармоники. Во втором случае (рис. 4-8, б) имеем ряд:
pi(t)
=
p0+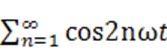 
, (4-22)
содержащий только четные гармоники. Этим двум разложениям как раз и соответствуют изменения параметров в нечетно- и четногармонйческих преобразователях.
Подставив (4-21) в (4-5), найдем спектр полезной э. д. с. нечетно-гармонического преобразователя. Этот спектр также содержит нечетные гармоники, поскольку В0 = const, а операция дифференцирования не приводит к возникновению четных гармоник. Спектр помехи, появляющейся на выходе преобразователя из-за непосредственных или опосредствованных наводок (цепи наводок показаны на рис. 4-7 штриховыми линиями) содержит первую гармонику и сумму четных гармоник. Спектр четных гармоник нетрудно получить, если умножить каждый член ряда (4-21) на sin ωt. Графически это умножение показано на рис. 4-8, а, справа.
Из общего спектра выходной э. д. с. нечетногармонических преобразователей обычно выделяют первую гармонику, поскольку чувствительность преобразователя по более высоким гармоникам мала. Для первой гармоники выходного напряжения можно записать:
е1(t) = S1Bi cos ωt + 
0 cos ωt, (4-23)
где
S1 =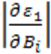 
= 
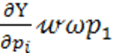
— чувствительность преобразователя по первой гармонике, полученная с учетом выражения (4-5).
Как следует из (4-23), полезный сигнал и помеха имеют одну и ту же частоту, вследствие чего отделить сигнал от помехи весьма затруднительно.
Спектр полезной э. д. с. в четногармоническом преобразователе может быть найден, если в (4-5) подставить (4-22). Очевидно, что этот спектр будет также содержать четные гармоники, поскольку в результате дифференцирования нечетные гармоники возникнуть не могут. Спектр же помехи, напротив, будет содержать только нечетные гармоники, что нетрудно получить, умножив каждый член ряда (4-22) на sin ωt. Графически умножение показано на рис. 4-8, б, справа.
Из общего спектра выходной э. д. с. четногармонйческих преобразователей обычно выделяют вторую гармонику. Поскольку спектр помехи содержит нечетные гармоники, то для второй гармоники выходной э. д. с, пренебрегая шумами, получаем
e2(t)=S2Bicos2ωt, (4-24)
где
S2 =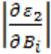 
= 
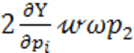
— чувствительность преобразователя по второй гармонике.
Таким образом, на выходе четногармонических преобразователей помеха с частотой второй гармоники отсутствует 1.
По этой причине четногармонические преобразователи менее подвержены смещению нуля и имеют более низкий порог чувствительности, чем нечетногармонические преобразователи.
В основе получения четной зависимости pi = f(t), как правило, лежит тот или иной четный эффект. Рассмотрение этих эффектов требует конкретного анализа, так как сами эффекты могут быть основаны на различных физических явлениях и законах. Рассматривая каждый тип активного индукционного преобразователя в соответствии с классификацией, данной в § 4-1, мы будем рассматривать нечетные и четные эффекты, лежащие в основе нечетногармонических и четногармонических преобразователей.
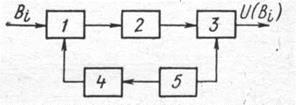
Рис. 4-9. Схема преобразования
1 – активный индукционный преобразователь; 2 – избирательный усилитель;
3 — синхронный детектор; 4 – фильтр нижних частот; 5—генератор накачки
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.