Магнитометрические преобразователи, приборы, установки, страница 11

Прежде всего на все четыре параметра может оказывать воздействие вибрация. Последняя проявляется не только при измерении с подвижных платформ (самоле­тов, катеров и т. п.), но и в стационарных условиях при сейсмическом или акусти­ческом воздействии.

Если вибрация приводит к угловым колебаниям преобразователя, то в соответ­ствии с формулой (4-6) возникает э. д. с. значение которой пропорционально попе­речной компоненте магнитной индукции внешнего постоянного поля.

Если же вибрация воздействует на параметры S и N, то в соответствии с форму­лами (4-8) и (4-10) возникает э. д. с. пропорциональная продольной компоненте постоянного поля.¹

Таким образом, ложный сигнал, появляющийся в пассивных преобразователях, зависит как от поперечной, так и от продольной компоненты постоянного поля. В поле Земли с индукцией порядка 50 мктл ложный сигнал, обусловленный вибра­цией, может во много раз превышать уровень собственных шумов пассивного пре­образователя.

Очевидно, что в тех случаях, когда уровень помех значителен, добиваться низ­кого уровня собственных шумов пассивного преобразователя не имеет смысла.

4-3. Проницаемость сердечников

В § 4-1 указывалось, что магнитная проницаемость сердечников, используемых в индукционных преобразователях, характеризуется тензором. Будучи приведен­ным к главным осям (х, y, z), этот тензор в соответствии с (4-2) имеет компоненты:

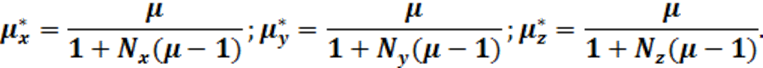
Если сердечник имеет форму вытянутого эллипсоида (овоида) с продольной осью х и поперечными осями у я z (рис. 4-2, в), то справедливо соотношение:

N_x + N_y+ N₂= 1.

При этом,

Nx =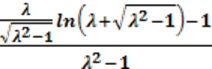

И N_y=N_z=(1-N_x)/2, где λ=x/y=x/z; x,y,z – длина полуосей или осей эллипсоида.

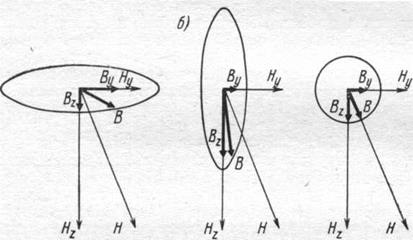
Рис. 4-3. Ферромагнитные эллипсоид и шар в магнитном поле

При λ > 10 N_X < 0,02, a N_y и N_z находятся в пределах 0,490,5. Подставляя значения, видим, что наибольшую проницаемость вытянутый эллипсоид имеет в на­правлении большой оси (оси х).

Если произвольно ориентировать такой эллипсоид относительно вектора напря­женности слабого внешнего поля, то получим

B_x= H_x; B_y= H_y; B_z= H_z;

где Н_х, Н_у, Н_z — компоненты вектора Н и В_х, В_у, B_z — соответствующие компо­ненты вектора В внутри эллипсоида. Модули векторов Н и В будут

H =,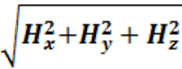

B = µ₀.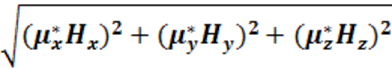

Из-за различия значений  отношение

т. е. вектор В оказывается непараллельным вектору Н.

При произвольной ориентации эллипсоида вектор В отклоняется от вектора Н в сторону большой оси (рис. 1-3, а и б). Если ориентация неизменна, то это отклоне­ние тем сильнее, чем значительнее величина λ отличается от единицы.

Когда λ = 1 эллипсоид вырождается в шар. Для шара N_x= N_у = N_z= ¹/₃ и . Поэтому, вектор В в нем всегда параллелен вектору Н (рис. 4-3, в).

При λ  1, например, при λ = 100, N_x = 4,3∙10^-4. Положив λ = 10⁵, имеем:  2,3∙10³ и , т. е. в направлении большой оси проницаемость эллип­соида оказывается на три порядка выше, чем в направлении малой оси. В этом слу­чае вектор В практически совпадает с направлением большой оси и компонентой В_х, так как компонентами В_у и B_z, ввиду их малости, можно пренебречь.

Полученный результат чрезвычайно важен. Он свидетельствует о том, что вытя­нутый эллипсоид, изготовленный из вещества с высокой магнитной проницаемостью, фактически намагничивается под действием составляющей внешнего поля, совпадаю­щей с направлением его продольной оси.

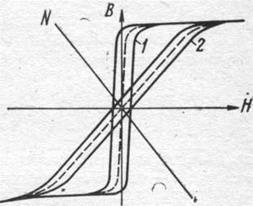
Рис. 4-4. Предельные гистерезисные петли и

средние кривые намагничивания

вещества (1) и тела (2)

Направленные свойства преобразователей с ферромагнитными сердечниками, таким обра­зом, обусловлены не только расположением изме­рительной катушки (единичным вектором s°), но и сильно выраженной анизотропией формы сер­дечников. Как уже отмечалось в §4-1, на прак­тике используют случай, когда s° || .

Несмотря на то, что продольная проницае­мость вытянутого эллипсоида во много раз боль­ше поперечной, она всегда меньше проницае­мости вещества, из которого изготовлен этот эллипсоид.

Для получения больших значений индук­ций обычно стремятся к тому, чтобы проницае­мость тела оказалась близкой к проницаемости формы, т. е. к выполнению условия µ^*m. Однако выполнение этого условия имеет и более глубокий практический смысл.

Из (4-2) следует, что при заданном N ∆µ* = ∆µ, где ∆µ — приращение проницаемости вещества и ∆µ* — приращение проницаемости тела. Взяв логарифми­ческую производную от (4-2) с учетом того, что µ  1, получим

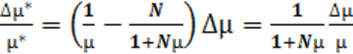                                                                              (4-14)

Равенство (4-14) показывает, что относительные приращения проницаемости тела ослаблены в 1 + Nµ раз по сравнению с вызывающими их относительными при­ращениями проницаемости вещества.

Заметим, что коэффициент N может рассматриваться как показатель глубины отрицательной обратной связи в теле. Чем ближе расположены в теле магнитные полюсы, тем больше коэффициент N и, следовательно, глубже обратная связь. Раз­личием глубины обратной связи в направлении трех главных осей как раз и объяс­няется магнитная анизотропия ферромагнитных тел.

При выполнении условия Nµ  1 обратная связь в соответствии с (4-14) ста­новится настолько глубокой, что индукция в теле оказывается величиной, почти не зависящей от изменения проницаемости вещества. Эта неизменность индукции и воспринимается как неизменность проницаемости тела по отношению к внешнему полю.

Аналогичным образом может быть объяснена и скошенность гистерезисной петли тела (сдвиг Релея) относительно гистерезисной петли вещества. Скошенность тем сильнее, чем больше коэффициент N и, следовательно, глубже обратная связь. Из-за наличия последней тем же значениям индукции соответствуют большие напряжен­ности поля  (рис. 4-4).

Из полученных выражений следует, что для нахождения параметров индукцион­ных преобразователей с сердечниками необходимо знать их коэффициенты размагни­чивания. Эти коэффициенты достаточно просто вычисляются для сердечников эллипсоидальной формы. Однако изготовление сердечников в форме эллипсоидов сопряжено со значительными трудностями. В индукционных преобразователях, как правило, используются сердечники неэллипсоидальной формы, выполненные, например, в виде вытянутых цилиндров (стержней) или полосок прямоугольного сечения (штам­пованных пластинок).