Указанные четыре типа активных преобразователей (см. рис. 4-1), очевидно, могут быть отнесены к разряду модуляторных устройств. Модуляция (перенос спектра измеряемого поля в область более высоких частот) осуществляется в этих преобразователях за счет принудительного воздействия на соответствующий частный параметр.
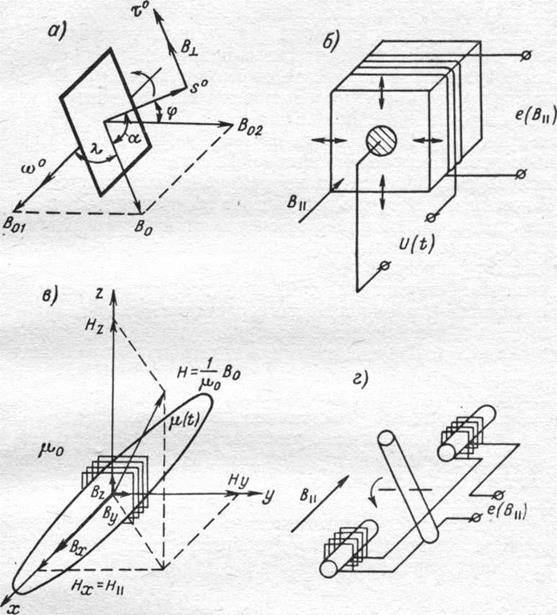
Рис. 4-2. Типы активных индукционных преобразователей: α-преобразователь (а); s-преобразователь (б); µ - преобразователь (в); N – преобразователь (г)
Поскольку в слабых полях Y
f
(В0), то все
четыре типа преобразователей могут рассматриваться как параметрические
устройства.
Наиболее характерные схемы каждого типа преобразователя изображены на рис. 4-2.
В качестве α-преобразователя
показана вращающаяся рамка, составляющая чувствительную часть широко
распространенного прибора, называемого измерительным генератором. Уравнение
(4-6), характеризующее работу такого преобразователя, может быть записано
иначе, если вместо α ввести углы
λ = 
и φ = 
(рис. 4-2, а). С учетом
равенств ds0/dt = τ°dφ/dt, τ° 
s° и ω° = [s° τ°] =
const получаем (при µ = 1):
e[s°(t)]
= -ωsB0 
= ωsB0 sin λsinφ
(4-10)
Примером s-преобразователя может служить струнный преобразователь, а также преобразователь, изображенный на рис. 4-2, б. В последнем контур закреплен на гранях пьезокристалла. При подведении к обкладкам электрического напряжения кристалл деформируется (обратный пьезоэффект), деформируя контур. В результате деформации площадь контура изменяется и в нем возникает э. д. с, пропорциональная индукции внешнего поля.
Примером µ-преобразователя служит феррозонд. В феррозондах изменение проницаемости материала (вещества) сердечников осуществляется за счет наложения на них вспомогательного магнитного поля. Заметим, однако, что воздействие на µ может осуществляться и иными способами, например за счет механического сжатия и т. д. Во всех случаях механизм преобразования в µ -преобразователях описывается уравнением (4-8). Данный тип преобразователя схематически показан на рис. 4-2, в. Из этого же рисунка очевиден смысл тензора магнитной проницаемости сердечника.
Примером N-преобразователя служит устройство, изображенное на рис. 4-2, г. Здесь вращение ферромагнитного ротора относительно неподвижного ферромагнитного статора, на котором размещены измерительные катушки, может рассматриваться, как периодическое изменение коэффициента размагничивания ферромагнитной системы. Очевидно, что в данном типе преобразователя вращательное движение может быть заменено поступательным. Кроме того, коэффициент N может изменяться в сплошных сердечниках за счет магнитоупругих свойств вещества (магнитострикция, термострикция и т. п.).
Различные способы энергетического воздействия на конкретные параметры, определяющие тип преобразователя, рассматриваются в последующих параграфах.
4-2. Пассивные индукционные преобразователи
Основное уравнение пассивного преобразователя может быть получено из уравнений (4-3) и (4-4). С учетом сделанных ранее замечаний оно имеет вид:
e[B0(t)] = -ω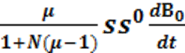
(4-11)
Пассивный преобразователь реагирует на скорость изменения внешнего поля В0. При этом внешнее поле может изменяться как по модулю, так и по направлению. В обоих случаях в неподвижно установленном преобразователе возникает э. д. с.
Если внешнее поле изменяется только по модулю, то взамен (4-11) можно написать:
e[B0(t)] = -ω
(4-12)
где α = 
.
При произвольном характере изменения измеряемого поля передаточные свойства пассивного преобразователя должны выражаться через динамическую чувствительность (см. § 2-2), в частности, можно пользоваться, например, передаточной функцией S(р) = Ap/Ω, где А = ωsµ( [ 1 + N (µ-1)] — постоянный коэффициент и Ω — круговая частота изменения модуля В0.
Когда модуль В0 изменяется по заданному закону, например: В0(t) = ВоmsinΩt передаточную характеристику пассивного преобразователя можно описать коэффициентом, который в § 2-2 назван нами квазистатической чувствительностью:
, (4-13)
где εm — амплитуда выходной э. д. с. преобразователя. Квазистатическая чувствительность пассивного преобразователя, очевидно, тем выше, чем больше частота изменения модуля В0.
Расчет пассивных индукционных преобразователей, как правило, сводится к обеспечению заданной чувствительности на нижней граничной частоте измеряемого поля, к определению комплексного выходного сопротивления, а также к оценке постоянства параметров s° , S, µ и N. Последнее необходимо для того, чтобы учесть уровень ложного сигнала, появляющегося в преобразователе при наличии постоянного магнитного поля (магнитного поля Земли) в соответствии с уравнениями (4-6)-(4-9).
Чувствительность пассивного преобразователя выбирают, исходя из заданного рабочего диапазона измерительного устройства и шумов (включая флуктуации нуля) модулятора или усилительного каскада, с которым непосредственно согласуется преобразователь.
Наиболее эффективный способ повышения чувствительности — увеличение числа витков измерительной катушки и использование сердечников из высокопроницаемых материалов (феррита, пермаллоя и т. п.). При этом, необходимо помнить, что увеличение числа витков вызывает резкое увеличение выходного (индуктивного) сопротивления, применение же сердечников с очень высокой проницаемостью приводит к непостоянству чувствительности преобразователя, а также зависимости чувствительности и выходного сопротивления от воздействия постоянных магнитных полей.
Вопросам расчета и согласования пассивных преобразователей с нагрузкой (входной частью усилительно-преобразовательной схемы) посвящен ряд работ [4-2 - 4-4].
Особое внимание при проектировании пассивных преобразователей должно уделяться анализу постоянства параметров s°, S, µ и N, так как при их изменении и при наличии постоянных магнитных полей возникает ложный сигнал.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.