В установившемся состоянии обе
силы F1 и
F2 равны по абсолютному значению
и противоположны по направлению. Таким образом, приравняв правые части уравнений
(1-12) и (1-13) и переходя к скалярной форме записи, получим выражения для
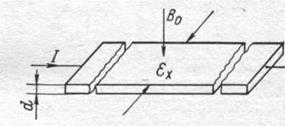
напряженности электрического поля Холла, названного в § 1-1 «полем движения»
Ex = vB0. (1-14)
На практике удобнее пользоваться выражением для э. д. с. Холла через ток / и геометрические размеры пластины. Поскольку напряженность электрического поля Ex= ξх/a, а ток I = ne0υad, где а — ширина пластины; d — ее толщина; п — концентрация носителей заряда, то с учетом этих соотношений формулу (1-14) можно записать так:
ξх = RxIB0/d (1-15)
где Rx = 1/(e0n) — коэффициент, зависящий только от природы вещества, из которого изготовлена пластина, 'и называемый коэффициентом или постоянной Холла.
Выражение (1-15), полученное на основании элементарных представлений электронной теории, строго говоря, справедливо только в случае идеальных проводников, когда скорость всех электронов можно считать одинаковой. В реальных веществах благодаря тепловому движению в токе участвуют электроны с самыми разнообразными скоростями. В этом случае постоянная Холла будет зависеть от того, какова при данной скорости продолжительность между двумя столкновениями или какова при этом длина свободного пробега электрона, что, в свою очередь, зависит от типа кристаллической решетки. Влияние типа решетки учитывается с помощью коэффициента А, т. е.
Rx = А/(е0п). При изготовлении гальваномагнитных преобразователей наиболее часто используются полупроводники, имеющие атомную решетку, для которой А = Зπ/8, т. е.
Далее, выражение (1-15) получено в предположении, что в переносе тока участвуют только заряды одного знака: дырки или электроны. Вместе с тем имеются полупроводники, в проводимости которых участвуют как дырки, концентрацию которых обозначим через р, а подвижность через ир, так и электроны с концентрацией п и подвижностью и. Для таких полупроводников значение постоянной Холла может быть определено по формуле
---------- 
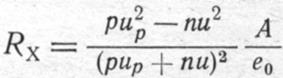--------------- (1-16)
Если проводящая пластина
питается не от источника тока, а от источника напряжения, то, выражая ток I в формуле (1-15) через
приложенное напряжение U и проводимость 
(где 
— удельная проводимость, s = ad — площадь сечения пластины; а и d — ее ширина и длина) и
производя необходимые сокращения, получим
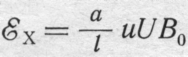(1-17)
Как видно из последнего выражения, в этом случае э. д. с. Холла, пропорциональна подвижности носителей заряда, а не постоянной Холла.
Перейдем теперь к рассмотрению
эффекта, заключающегося в увеличении продольного сопротивления проводника в
магнитном поле (эффект магнитосопротивления). Согласно наиболее простым представлениям
о движении электронов в проводнике, полагающим одинаковую скорость движения
всех электронов, магнитное поле не должно было бы влиять на сопротивление
проводника. Действительно, поскольку силы, действующие на отдельные электроны
со стороны магнитного поля и поперечного электрического поля Холла, равны по
абсолютному значению и противоположны по направлению, то электрон внутри
пластины должен был бы двигаться строго по прямой (таким образом, поле Холла,
вообще говоря, препятствует изменению сопротивления проводника). На самом деле,
так как существует определенное распределение электронов по скоростям
(распределение Ферми—Дирака), то равенство F1 = F2 выполняется только для
электронов, двигающихся с некоторой средней скоростью υср.
Электроны, двигающиеся со скоростями меньше и больше υcp, будут отклоняться против или
по направлению электрического поля. Следовательно, электроны, у которых v
vcp пройдут в единицу времени
меньший путь вдоль проводника, что эквивалентно увеличению его сопротивления.
Современная теория эффекта магнитосопротивления дает следующие выражения для относительного изменения удельного сопротивления ∆ρ/ρ полупроводников с атомной решеткой и одним знаком носителей заряда:
(1-18)
Где 1 ≤ n ≤ 2.
В слабых магнитных полях, когда иВ0 << 1, п = 2; в более сильных полях, для которых иВ0 > 1, п лежит в пределах от 1 до 2. Кроме того, как будет показано в § 5-7, на характер зависимости ∆ρ/ρ = f(В0) существенное влияние оказывает форма проводящей пластины.
В большинстве полупроводников эффект магнитосопротивления проявляется значительно сильнее, чем в проводниках. Объясняется это большей подвижностью носителей заряда, а также наличием наряду с электронной и дырочной проводимости. Так как дырки движутся в полупроводнике в сторону, противоположную движению электронов, то направления лоренцовых сил, действующих на электрон и дырку, совпадают. Отклоняясь к тому же краю пластины, что и электроны, дырки, естественно, уменьшают скапливающийся заряд, поле Холла и силу F2. Нарушение равновесия сил F1 и F2 и приводит к дополнительному искривлению траектории движения заряда. Если бы подвижность дырок и электронов была одинаковой, то при равной их концентрации (что, например, выполняется у собственных полупроводников) постоянная Холла, как это следует из формулы (1-16), была бы равна нулю и поле Холла вообще бы не возникало. Эффект магнитосопротивления при прочих равных условиях в этом случае должен проявляться наиболее сильно. На практике у большинства полупроводников подвижность дырок намного меньше подвижности электронов, так что в ряде случаев их влиянием можно пренебречь.
Из всех физических явлений, используемых в магнитометрии, особо следует выделить явление магнитного резонанса, заключающееся в избирательном поглощении или излучении электромагнитных волн веществом, помещенным в магнитное поле. В зависимости от природы элементарных частиц, участвующих в процессе резонансного поглощения или излучения энергии, различают электронный парамагнитный резонанс и ядерный магнитный резонанс.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.