Феррозонды, работающие в первом режиме, относятся к преобразователям с выходом на основной частоте. Феррозонды, работающие во втором режиме, являются четногармоническими преобразователями. Ввиду явных преимуществ четногармонических преобразователей, в дальнейшем мы будем говорить главным образом о втором режиме работы феррозондов.
Независимо от выбранного режима работы феррозонды могут быть разделены по способу наложения вспомогательного переменного поля.
4-10. Феррозонды с продольным возбуждением
Изобретение феррозондов связывают с именами немецких ученых – Ашенбреннера и Губо [4-41], хотя в отдельных источниках упоминаются и другие имена. Ашенбреннером и Губо был предложен и опробован феррозонд кольцевого типа (рис. 4-20). В качестве сердечника они использовали железную («цветочную») проволоку, покрытую шеллаком. Обмотка возбуждения наматывалась непосредственно на сердечник, измерительная обмотка размещалась на специальном каркасе. Использовался второй режим работы, при этом измерительная обмотка настраивалась в резонанс на частоту второй гармоники. Э. д. с. второй гармоники была пропорциональна компоненте поля Bi, действующей в направлении ММ' т. е. по нормали к плоскости витков вторичной обмотки.
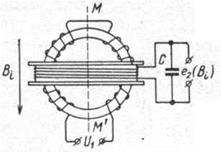
Рис. 4-20. Феррозонд Ашенбреннера и Губо
Феррозонды Ашенбреннера и Губо были усовершенствованы Ферстером [4-6, 4-42], который взамен кольцевого сердечника использовал два раздельных стержневых сердечника. Феррозонд с двумя сердечниками получил наибольшее распространение и применяется до настоящего времени.
Независимо от Ферстера и примерно в то же время стержневые феррозонды были предложены и опробованы П. А. Халилеевым в Советском Союзе [4-19, 4-40].
Несмотря на сравнительную давность изобретения феррозондов, сколько-нибудь цельная и последовательная теория их, положенная в основу анализа и расчетов, появилась значительно позднее. Разработке теории немало способствовали советские ученые. Основополагающим явилось учение о намагничивании ферромагнитных тел конечных размеров, развитое крупным советским физиком В. К. Аркадьевым [4-1 ]. Это учение использовано во всех отечественных и зарубежных работах по феррозондам. Большой вклад в теорию феррозондов внесли М. А. Розенблат [4-7] и Р. И. Янус [4-43]. Более подробный список авторов и работ дан в [4-40].
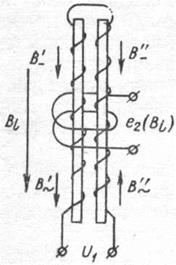
Рис. 4-21. Дифференциальный феррозонд
Найдем выражение для чувствительности наиболее распространенного двухстержневого (дифференциального) феррозонда, схема которого приведена на рис. 4-21. Феррозонд выполнен в виде двух ферромагнитных (пермаллое-вых) сердечников с распределенными по их длине первичными, включенными последовательно — встречно, и общей вторичной обмотками. Встречное включение первичных обмоток приводит к тому, что в отсутствие измеряемого поля Bi э. д. с, наводимая во вторичной (измерительной) обмотке, близка к нулю. При наличии же измеряемого поля баланс между потоками в первом и втором сердечниках нарушается и во вторичной обмотке появляется э. д. с, пропорциональная продольной компоненте внешнего поля.
Воспользуемся однозначной
кривой перемагничивания, показанной на рис. 4-4 штриховой линией. Поскольку
векторы постоянного и переменного полей в каждом сердечнике параллельны или
анти-параллельны, однозначную нелинейную зависимость В(Н1
H0), где Н1 и Н0 — напряженности вспомогательного (переменного) и
измеряемого (постоянного, Н0 = Bi/µ0) магнитных
полей соответственно, можно разложить в ряд Тейлора. Для второго режима работы
(Н1 
Н0), ограничиваясь тремя членами
ряда, получаем:
B' = B(Н1,+ Н0) = µ0[µ*Н1+
Н0
- 
]
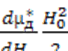(4-37)
B"
= B(Н1,- Н0) = µ0[-µ*Н1+
Н0+
]
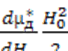где В'
и В" - значения суммарной индукции
в первом и втором сердечниках; µ* = B/µ0H и µ*
= dB/µ0dH – нормальная и дифференциальная
относительные магнитные проницаемости сердечников соответственно. Связь между µ* и 
дается соотношением:
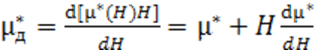(4-38)
Отсюда нетрудно заключить, что
= µ*
только
тогда, когда Н
= 0 или dµ*/dH = 0. Во всех других случаях 
µ*.
Очевидно, что зависимость 
(Н)
характеризуется
гораздо большей нелинейностью, чем зависимость µ*(H). Совпадая с нормальной проницаемостью
в области слабых полей, дифференциальная проницаемость резко падает при
насыщении сердечника, оказываясь в сотни раз меньше нормальной.
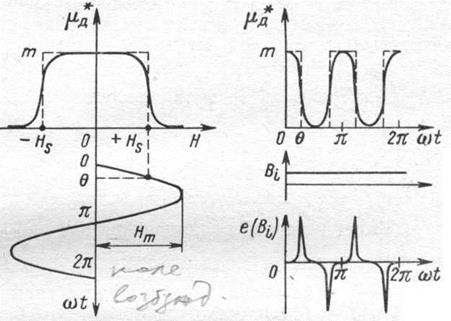
Рис. 4-22. Эпюры, поясняющие работу феррозонда с продольным возбуждением
Э. д. с, наводимая в
измерительной обмотке феррозонда, очевидно, будет: е=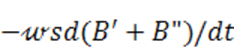
. Отсюда с учетом (4-37) получаем:
е = 
, (4-39)
где Bi = µ 0H0, 
– число витков измерительной обмотки и s –
площадь
поперечного сечения одного сердечника.
Из (4-39) следует, что э. д. с. двухстержневого феррозонда с продольным возбуждением пропорциональна скорости изменения относительной дифференциальной проницаемости сердечников.
Если сердечники возбуждаются
синусоидальным переменным током, достаточным для их насыщения, то характер
изменения (ωt) будет иметь вид, показанный на рис. 4-22. Там же
показана и зависимость е
(ωt) 
d
/dt. Видно, что на участке ωt =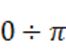 
/2. Эта зависимость не остается постоянной. При ωt 
0 и ωt 
/2 значение d /dt стремится к нулю, при ωt θ, где θ — так называемый угол насыщения
сердечников, значение dµ*/dtдостигает максимального значения. По этой причине
форма выходной э. д. с. е(В ) даже при наличии близкого к
нулю значения Bi, как правило, отлична от синусоидальной и имеет вид
острых пиков (рис. 4-22).
Ввиду несинусоидального характера выходной э. д. с, чувствительность феррозонда может быть оценена по среднему значению выходной э. д. с, пиковому значению или по амплитуде одной из четных гармоник [4-43, 4-44]. Поскольку наибольшее распространение получили схемы магнитометров, в которых полезный сигнал несет одна из четных гармоник, найдем чувствительность феррозонда по амплитуде четных гармоник.
Очевидно, что функция (H) – четная. Если H1(ωt) =
Н1
sin ωt, где Н1 — амплитуда поля возбуждения,
то при Н0 
0, в соответствии с изложенным в §4-4, имеем
[4-45—4-47]:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.