Магнитометрические преобразователи, приборы, установки, страница 12

Трудность вычисления коэффициентов размагничивания подобных тел объяс­няется тем, что строгих аналитических выражений, связывающих значения коэф­фициентов с геометрическими размерами, не существует. Подобные тела, приобре­тая во внешнем однородном поле неоднородную намагниченность, характеризуются в различных точках тела и различными значениями размагничивающего поля. Поэтому, применительно к таким телам можно говорить лишь о некоторых усреднен­ных для данного участка или всего сердечника в целом коэффициентах размагни­чивания.

В работе М. А. Розенблата [4-5] показано, что центральный коэффициент размагничивания сплошных и полых цилиндров, сплошных и наборных стержней прямоугольного сечения, а также эллипсоидов может быть вычислен по формуле

N_ц =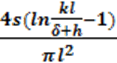                                               (4-15)

где s — площадь поперечного сечения сердечника (для эллипсоидов в экваторном сечении); l— длина сердечника, δ и h — поперечные размеры сердечника и k– коэффициент, зависящий от формы сердечника

Для цилиндра (k  = 2,4, δ = h= d) получаем

N_ц∙ц=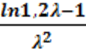                                                  (4-16)

Часто пользуются упрощенной формулой   [4-6, 4-7]:

N_ц                                                                           (4-17)

которая, однако, справедлива лишь для случая, когда ln. Формула (4-17) пригодна лишь для прикидочных расчетов. Для более точных расчетов следует поль­зоваться формулой (4-15).

Пользуясь центральными коэффициентами размагничивания, с учетом N_µ  1 и ранее сделанных допущений, находим центральное значение B_ц индукции в сер­дечниках

B_ц=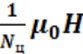                                                      (4-18)

В сердечниках неэллипсоидальной формы значение В_ц является наибольшим из всех других значений индукции, взятых по длине сердечника (рис. 4-5). Задав­шись законом распределения индукции вдоль сердечника, можно определить ее среднее значение В_ср и, следовательно, найти усредненные коэффициенты размаг­ничивания. Усредненные коэффициенты размагничивания как раз и нужны для практических расчетов.

Если участок усреднения расположен симметрично относительно центрального сечения сердечника, то [4-7]

N_y = 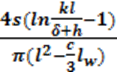,                                                         (4-19)

где l_w = x₂ - x_l — длина участка усреднения или размещенной на нем обмотки.

Формула (4-19) носит универсальный характер. Она пригодна для расчета коэффициентов размагничивания сердечников эллипсоидальной, цилиндрической и призма­тической форм. Пользуясь ею, можно вычислять как дроссельные (l_w < l) так и магнитометрические (l_w = l) коэффициенты размагничивания. Некоторым недо­статком формулы может служить лишь наличие в ней табличных коэффициентов k и с.

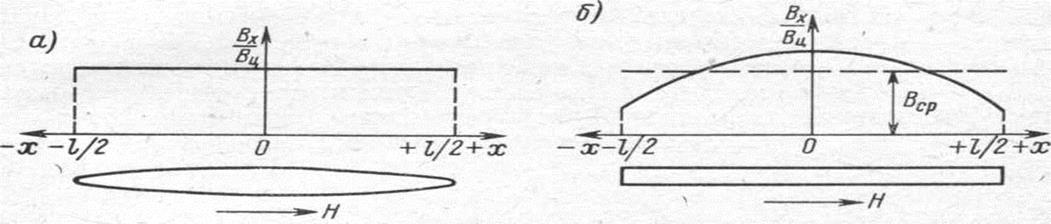
Рис. 4-5. Распределение внутренней индукции вдоль

длины эллипсоидаль­ного (а)и прямоугольного (б) сердечников

Пользуясь формулой (4-19) и выражением (4-14), можно определить условия, при которых проницаемость сердечников µ* оказывается стабилизированной. Далее, легко определить и саму величину µ*: при N_yµ  1 она равна 1/N_y.

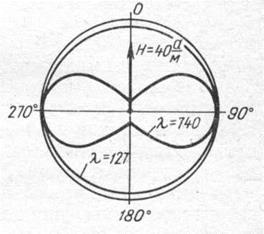
Рис. 4-6.Зависимость чувстви­тельности преобразователя сферромагнитным сердечником при изменении ориентации относи­тельно вектора Н

Приведенные в настоящем параграфе формулы могут быть использованы как для расчетов проницаемости сердечников, а следовательно, и чувствительности индукционных преобразователей, так и для оценки постоянства чувствительности при воз­действии на преобразователь внешних факторов. Соотношение (4-14) остается справедливым, неза­висимо от того, под действием каких факторов изменяется относительная магнитная проницае­мость вещества сердечника. Магнитная проницаемость может изменяться под действием меха­нических напряжений, изменения температуры окружающей среды, при наличии паразитных (неизмеряемых) внешних магнитных полей.

На рис. 4-6 показано, в частности, как изме­няется чувствительность пассивного преобразо­вателя при поворотах в магнитном поле Земли в зависимости от значений λ=l/d используе­мых в нем пермаллоевых сердечников [4-8]. Видно, что при λ = 740(µ*  9∙10⁴ и ориентации преобразователя вдоль вектора Н его чувствительность примерно на порядок ниже, чем при взаимно перпендикулярном расположе­нии сердечника преобразователя и вектора Н. При λ = 127 (µ* 4∙10³) чувствительность преобразователя от ориентации почти не зависит.

При заданном значении Н и известной зависимости µ(Н), можно, не прибегая каждый раз к экспериментам и построению годографов чувствительности преобразователя (рис. 4-6), пользуясь только соотношением (4-14), найти λ или N, при которых изменение чувствительности за счет произвольной ориентации пре­образователя не превысит расчетно допустимых значений.

Погрешность, обусловленная влиянием механического напряжения, темпера­туры окружающей среды и постоянного внешнего поля носит, очевидно, сугубо мультипликативный характер.

4-4. Активные индукционные преобразователи (нечетногармонические и четногармонические)

Активные индукционные преобразователи отличаются от пассив­ного тем, что в них один из параметров (s°, s, µ или N) изменяется принудительно. Принудительное воздействие на параметр сопря­жено с затратой дополнительной энергии. Схема активного преобра­зователя поэтому имеет вид, показанный на рис. 2-1, б. В качестве дополнительной, как правило, используется электрическая энергия.

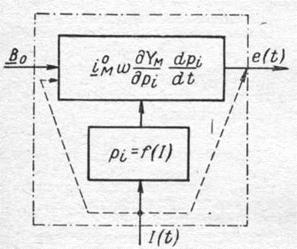
Рис. 4-7. Структурная схема активного индукционного преобразователя

В § 4-1 отмечалось, что активные индукционные преобразователи могут рассматриваться как параметрические устройства. Из теории параметрических преобразователей известно [4-9—4-13], что в них возможна модуляция и усиление сигнала по мощности. Модуляция возможна благодаря перемножению входной (измеряемой) величины с изменяющимся во времени параметром. Модуляция или перенос спектра частот входного сигнала «вверх» осуществляется тогда, когда частота изменения параметра значительно выше верхней граничной частоты спектра сигнала. В соответствии с теоремой Мэнли-Роу [4-13], преобразование    «вверх» в реактивных параметрических преобразователях всегда сопро­вождается усилением сигнала по мощности. Модуляторные и усили­тельные свойства выгодно отличают активные индукционные пре­образователи от пассивных. Преимущества первых проявляются особенно ярко, когда они используются для преобразования инфранизкочастотных сигналов малой мощности. Однако активным пре­образователям присущи и недостатки.