Магнитометрические преобразователи, приборы, установки, страница 5

Явление электронного парамагнитного резонанса было открыто Е. К. Завойским в 1944 г. и сразу же привлекло широкое внимание как отечественных, так и зарубежных ученых. В 1946 году двум груп­пам научных работников, возглавляемых М. Ф. Блохом и Е. М. Пар-селлом, удалось независимо друг от друга обнаружить чисто радио­техническими средствами резонансное поглощение электромагнит­ной энергии ядрами водорода в воде и парафине — ядерный магнит­ный резонанс (ЯМР).

Сущность ЯМР может быть сравнительно легко объяснена с по­зиций квантовой механики. Как известно, система ядер, обладающих магнитными моментами, при помещении в магнитное поле имеет энер­гетический (зеемановский) спектр, состоящий из 2j + 1 равноот­стоящих энергетических уровней, где j — спиновое число, прини­мающее в зависимости от типа ядер целые или полуцелые значения. Известно далее, что каждый уровень характеризуется магнитным квантовым числом т, которое также принимает 2j+1 дискретных значения из ряда j, (j-1), …, -( j -1), - j. В частности, для протонов j=1/2, что соответствует двум энергетическим уровням со значениями т: т₁=1/2 и m₂=-1/2.

Разность значений энергии этих уровней зависит от значения магнитной индукции В. Например, для ядер водорода эта разность определяется соотношением

                                     ∆E=B,                                                                                   (1-19)

где h — постоянная Планка;  — гиромагнитное отношение — фундаментальная физическая константа, равная для протона 2,67510⁸ тл^-1сек^-1рад.

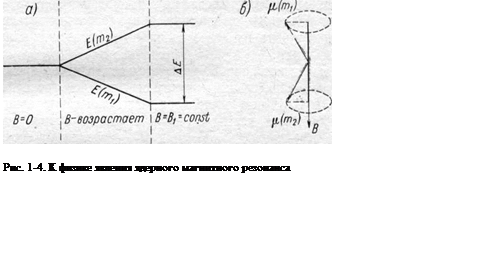
Как видно из соотношения (1-19), в отсутствие магнитного поля (при B = 0) энергетические уровни вырождены¹, а при наложении поля расщепление между обоими энергетическими уровнями линейно возрастает с ростом В (рис. 1-4, а).

Пользуясь формулой (1-19) и уравнением Больцмана для распре­деления отдельных ядер системы по энергетическим уровням, можно получить [1-5] отношение населенностей двух смежных уровней — нижнего N(m₁) и верхнего N(m₂):

,

где k — постоянная Больцмана; Т — абсолютная температура. Так как число ядер системы остается неизменным и равным N = N (m₁) + N (m₂), то увеличение населенности нижнего уровня, естественно, осуществляется за счет уменьшения населенности .верхнего уровня. В равновесном состоянии системы, наступившем при каком-то опре­деленном значении 5, согласно уравнению теплового баланса число переходов в единицу времени снизу вверх равно числу переходов сверху вниз, т. е. выполняется равенство

N(m₁)=N(m₂)                                 (1-20)

где и  — вероятности переходов между соответству­ющими уровнями в единицу времени.

Из сказанного очевидно, что обнаружить расщепление энерге­тических уровней ∆E = В можно только путем измерения частоты электромагнитного излучения или поглощения при переходе ядер или других частиц одного уровня на другой. Это, в свою очередь, может быть достигнуто только в одном случае: если созданы условия, при которых равенство (1-20) нарушается, другими словами, если число переходов снизу вверх больше числа переходов сверху вниз или наоборот.

Такие условия возникают, например, при воздействии на веще­ство со стороны высокочастотного электромагнитного поля. Как из­вестно из современного учения об элементарных частицах, при вне­сении отдельного протона, обладающего магнитным моментом µ и моментом количества движения Р в магнитное поле, момент µ будет прецессировать вокруг вектора В с угловой скоростью, определяемой формулой Лормора ω₀ = γВ. Аналогично ведут себя и все остальные ядра системы независимо от их энергетического уровня. Различие состоит лишь з том, что у ядер, находящихся на нижнем уровне, проекции µ на В совпадают с направлением В, а у ядер, находящихся на верхнем уровне, — противоположны направлению В (рис. 1-4, б).

Подвергнем теперь систему ядер, находящихся в постоянном маг­нитном поле, воздействию электромагнитного поля, имеющего круго­вую поляризацию в направлении, перпендикулярном В. Так как в соответствии с принципом Паули возможны переходы лишь между соседними энергетическими уровнями при изменении т на ±1, при­чем каждый такой переход сопровождается изменением энергии спи­новой системы на величину ∆Е = hf, то можно утверждать, что взаи­модействие между спиновой системой и электромагнитным полем наступает только в том случае, когда частота последнего имеет вполне определенное резонансное значение:

f=.                                                                                  (1-21)

При выполнении этого условия система ядер поглощает часть энергии, что сопровождается уменьшением населенности нижнего уровня. Вероятность переходов ρ_м, стимулированных электромаг­нитным полем, одинакова для обоих направлений. Однако так как N(m₁) > N (m₂), то число переходов вверх больше числа переходов вниз, т. е. происходит нарушение термодинамического равновесия, отражаемого выражением (1-20). Тем не менее поскольку спиновая система всегда стремится к термодинамическому равновесию, то про­исходит обмен энергией между спинами и решеткой, в результате которого ядра возвращаются с верхнего уровня на нижний. Таким об­разом, в то время как электромагнитное поле уменьшает избыток населенности нижнего уровня, взаимодействие с решеткой стремится восстановить этот избыток до прежнего уровня. Поэтому резонанс­ное поглощение происходит непрерывно. Если бы не было взаимо­действия между спиновой системой и решеткой, спустя некоторое время под действием электромагнитного поля населенности уровней стали бы равными и поглощение энергии прекратилось.

Неравновесную населенность уровней можно создать и другими способами. Например, с помощью сильного постоянного магнитного поля или резонансного света (метод оптической накачки).

Описанное выше явление ЯМР, возникающее при взаимодействии магнитных моментов µ, прецессирующих вокруг поля В, с высоко­частотным полем В₁, вращающимся в плоскости, перпендикуляр­ной В, может быть наглядно изложено и с позиции классической электродинамики.