Магнитометрические преобразователи, приборы, установки, страница 9

для второго гауссова положения

                                              ;                                  (3-11)

для первого ламонова положения

                                              ;                                 (3-12)

для второго ламонова положения

                                              ;                                 (3-13)

где р и q — постоянные коэффициенты; r — расстояние между цен­трами стрелки ns и отклоняющего магнита NS. В реальном магните значения р и q зависят от размеров магнита и от законов распределения магнитных масс, вследствие чего они получили названия коэф­фициентов распределения. Для тел, ограниченных поверхностями второго порядка (шар, эллипсоид), значения коэффициентов распре­деления могут быть вычислены, во всех остальных случаях они опре­деляются экспериментально.

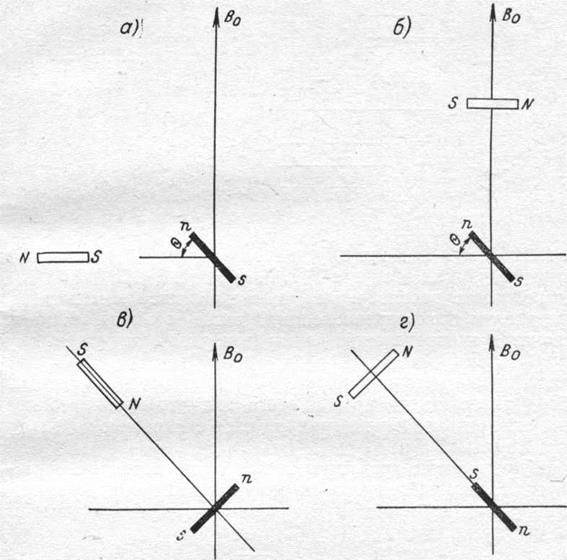
Рис. 3-9. Взаимное расположение магнитов

Период качания магнита в горизонтальной плоскости, находя­щегося в магнитном поле, определяется из уравнения (3-5), если положить р = 0 и :

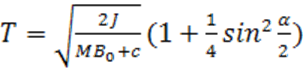                                              ,                                      (3-14)

где α — амплитуда колебаний магнита.

Значение модуля магнитной индукции может быть найдено в ре­зультате совместного решения относительно М и В₀ уравнения (3-14) и одного из уравнений (3-10)—(3-13). Например, решение уравне­ний (3-14) и (3-12) имеет вид [3-6]:

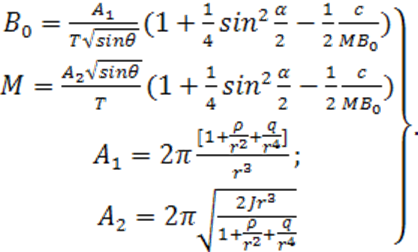                                                                    (3-15)

Как видно из (3-15), для определения В₀ необходимо произвести измерение следующих величин: T, r, , J, р, q и с/(МB₀).

Таким образом, рассмотренный метод является абсолютным, так как определение всех перечисленных выше величин в конечном счете сводится к определению длины (или угла), массы и времени [3-6].

Относительные методы измерения В₀ отличаются от рассмотрен­ного абсолютного метода прежде всего тем, что механический пре­образователь предварительно градуируется с помощью той или иной образцовой меры.

Например, процесс градуировки приборов, основанных на ме­тоде Гаусса, заключается в экспериментальном определении мно­жителя А₁ путем наблюдения полупериода T и угла θ в магнитном поле с известным значением В₀:

,

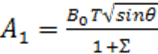где ∑ — сумма всех поправочных коэффициентов.

При относительном методе измерения отпадает необходимость в из­мерении расстояния между магнитами r, момента инерции J и коэф­фициентов распределения р и q. Необходимо только при наблюде­ниях устанавливать магнит всегда в одном и том же положении, чтобы иметь J и r постоянными.

Относительные методы измерения отличаются большей простотой и меньшей трудоемкостью, однако погрешность измерения относи­тельных методов, основанных на использовании механических пре­образователей, как правило, примерно на порядок ниже, чем абсо­лютного.

Глава   четвертая                            ИНДУКЦИОННЫЕ

                                 ПРЕОБРАЗОВАТЕЛИ

4-1. Классификация индукционных преобразователей

Как отмечалось в § 1-3, суммарная э. д. с, наводимая в контуре, может быть разделена на трансформаторную э. д. с. и э. д. с. движе­ния. Анализируя каждую из этих составляющих, можно провести дальнейшее разделение и выделить наиболее характерные типы ин­дукционных преобразователей.

Пусть имеется внешнее поле В₀, которое необходимо измерить. Поместим в это поле индукционный преобразователь. Будем считать также, что преобразователь в общем случае имеет сердечник, изго­товленный из вещества с относительной магнитной проницаемостью, отличной от единицы, т. е. µ 1. Тогда, если магнитное поле одно­родно, а сердечник имеет форму шара или эллипсоида вращения, маг­нитный поток через контур можно представить в виде: Ф = Bs = B₀-Y, где Y - обобщенный параметр преобразователя. В общем случае: В  В₀ и Y = f (В₀). Для слабых полей, когда возможна линеаризация начального участка кривой намагничивания,

Y = [µ^*]s (4-1)

Где [µ^*] - тензор относительной магнитной проницаемости сердечника.

      Тензор [µ^*] - симметричный. Его матрица имеет вид:

,

где , ,  — значения относительной проницаемости сердеч­ника в направлениях его главных осей (с которыми связана система координат х, у, z). Каждая компонента тензора может быть вычис­лена по формуле [4-1]:

                                              ,                                            (4-2)

где µ — относительная магнитная проницаемость вещества (пред­полагается изотропной); N — коэффициент размагничивания и i = х, у, z — индекс соответствующего направления.

В том частном случае, когда нормаль контура (ось измерительной катушки) s° совпадает с одной из главных осей сердечника следует учитывать только одну компоненту тензора. Так, если s° || х°, то следует учитывать лишь компоненту µ_x. Поскольку на практике условие s° || х°, где х° — продольная ось сердечника, почти всегда выполнимо, то с учетом (4-2) и представления s = s°s, где s — число, характеризующее площадь поперечного сечения контура, имеем вза­мен (4-1):

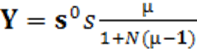                                              .                                                     (4-3)

Таким образом, обобщенный параметр преобразователя является функцией четырех частных параметров: s°, s, µ и N.

В соответствии с законом электромагнитной индукции э. д. с, наводимая в контуре с числом витков ω, будет:

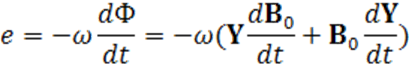
Очевидно, что когда Y = const, мы имеем дело с обычным пассив­ным преобразованием. Когда же В₀ = const, то преобразование воз­можно лишь за счет изменения параметра Y во времени. В первом случае э. д. с. пропорциональна скорости изменения самого поля; во втором — скорости изменения параметра.

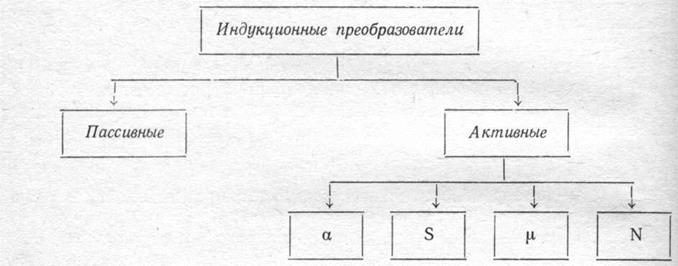
Рис. 4-1. Классификация индукционных преобразователей

Уравнение (4-4) позволяет разделить индукционные преобразо­ватели на две большие группы: пассивные и активные преобразова­тели,   (рис. 4-1).

Второй член уравнения (4-4) можно представить в виде:

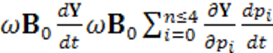,                                               (4-5)

где p_i= s°, s, µ, N — частный параметр преобразователя. Частные уравнения, отражающие процессы в соответствующих типах актив­ных преобразователей, имеют вид: