Магнитометрические преобразователи, приборы, установки, страница 3

Примером источника, генерирующего поле, изменяющееся во времени по модулю и направлению, служит катушка, питаемая пере­менным током частоты со и вращающаяся вокруг некоторой оси Ω° с частотой Ω.

В общем случае временные изменения магнитного поля могут носить периодический или апериодический характер. Периодические изменения  могут  быть   представлены  в   виде  ряда  Фурье   от двух переменных В и α, где α =  — угол между вектором и нормалью к плоскости витков пробной (воспринимающей) катушки. Апериодические изменения могут быть представлены в виде инте­грала Фурье от тех же переменных.

На практике чаще всего приходится иметь дело с асимметричными периодическими магнитными полями неизменного направления (В⁰ = const). В этом случае вектор-функция В (t) записывается в виде следующего ряда:

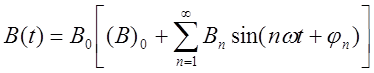,                                     (1-9)

где (В)₀  — постоянная составляющая магнитной индукции¹; В_п — амплитуда п-й гармоники магнитной индукции; со — круговая ча­стота периодического процесса; φ_n — начальная фаза п-й гармоники; п = 1, 2, 3, . . . — целые числа.

Часто пользуются также величиной dB/dt, характеризующей ско­рость изменения магнитного поля. В декартовой системе координат, очевидно, будем иметь

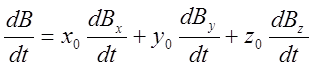
в сферической системе координат

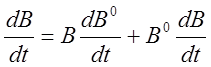
Принимая во внимание зависимость В = f (ψ, θ,В), из которой следует, что

В = F (ψ, θ), находим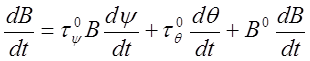

Если В⁰ = const и вектор-функция записывается в виде ряда (1-9), то

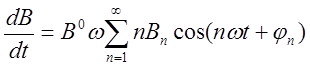
т. е. также записывается в виде ряда. При этом величина dB/dt ока­зывается пропорциональной частоте изменения поля, а каждый член ряда — номеру соответствующей гармоники.

Все рассмотренные в настоящем параграфе величины — недиф­ференциальные и дифференциальные — являются непосредственно изменяемыми или, точнее, непосредственно преобразуемыми вели­чинами. Они характеризуют не только структуру, но и временные изменения поля в некотором локальном объеме.

1-3. Физические явления и законы, используемые в преобразователях магнитной индукции

Как отмечалось в § 1-1, силовое взаимодействие магнита или эле­мента тока с исследуемым полем, а также электромагнитная индук­ция являются наиболее характерными и фундаментальными проявле­ниями магнитного поля. Именно эти проявления и были прежде всего использованы при конструировании измерительных преобра­зователей.

Простейшим и давно известным магнитометрическим преобразо­вателем, основанном на силовом взаимодействии, является свободно вращающаяся, подвешенная на нити или установленная на острие магнитная стрелка (применяется, например, в компасах). Механи­ческий вращающий момент, действующий на магнитную стрелку,

Р = [МВ₀], где М — магнитный момент стрелки. Написанное урав­нение есть результат интегрирования зависимости dF = I[dlB] (см. § 1-1), распространяемой на случай микроскопических токов в веществе.

Механические преобразователи, обладающие моментом инерции, по вполне понятным причинам не могли быть использованы для из­мерений в движении, а также для измерения параметров магнитных полей, быстро изменяющихся во времени. Наиболее перспективным методом, свободным от указанных недостатков, оказался индукцион­ный метод, основанный на явлении электромагнитной индукции, от­крытом Фарадеем. Закон электромагнитной индукции, обобщенный на случай движения контура или его части в магнитном поле, имеет вид:

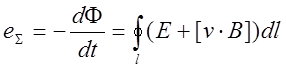
                    (1-10)

Выражение (1-10) отличается от ранее приведенного для э. д. с. движения e_дв наличием дополнительного члена, называемого транс­форматорной э. д. с,

е_тр =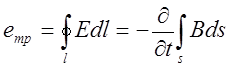

Если поле однородно, а контур плоский, то Ф = Bs и

                                                                          e_тр + е_дв = -(sdB/dt + Bds/dt)                                                                               (1-11)

откуда следует, что появление трансформаторной э. д. с. связано с изменением магнитного поля во времени, тогда как э. д. с. движения возникает за счет изменения эффективной площади контура.

В гл. 4 будет показано, что индукционные преобразователи могут быть построены на основе получения как э. д. с. движения, так и трансформаторной э. д. с.

Вскоре после открытия закона электромагнитной индукции были открыты еще несколько, по существу, родственных физических явле­ний (эффектов), возникающих в веществе, находящемся в магнитном поле, при прохождении через вещество электрического тока под действием электрического поля, и получивших название гальвано­магнитных.

В настоящее время известно четыре таких эффекта — два попе­речных и два продольных. Поперечный эффект Холла состоит в воз­никновении поперечной разности потенциалов (э. д. с. Холла), про­порциональной магнитной индукции и току, протекающему по про­воднику; эффект Эттингсгаузена — в появлении поперечной разности температур; эффект изменения сопротивления в магнитном поле — в изменении продольного сопротивления проводника и эффект Нернста — в появлении продольной разности температур.

Из четырех перечисленных эффектов в технике магнитных из­мерений широкое применение нашли только эффекты Холла и магнитосопротивления. На них мы остановимся более подробно.

Если по бесконечно длинной пластине, выполненной из проводя­щего материала и помещенной в магнитное поле (рис. 1-3), пропущен ток /, то на каждый электрон, движущийся внутри пластины, дей­ствует магнитная часть силы Лоренца F_1? пропорциональная заряду электрона и векторному произведению его скорости на магнитную индукцию В₀:

F₁ = е₀[vB₀].                  (1-12)

Под действием силы F_x электроны отклоняются к одному краю пластины, создавая там избыток отрицательных зарядов. Последнее обстоятельство приводит к появлению разности потенциалов ξ_х и, следовательно, поперечной составляющей напряженности электри­ческого поля Е_х. С появлением этой составляющей на электрон, кроме B₀ лоренцевой силы F_l9 начи­нает действовать также сила

F₂=e₀E_x.                 (1-13)