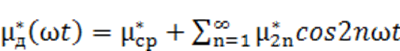Магнитометрические преобразователи, приборы, установки, страница 16

                                   ,                                  (4-40)

где   ⁼  – среднее значение (постоянная составляющая) дифференциальной проницаемости;  ⁼  – амплитуды четных   гармоник   проницаемости; n = 1, 2, 3, . . . —целые числа (номера четных гармоник).

Подставляя (4-40) в (4-39), находим

e(t)=.                                    (4-41)

Чувствительность феррозонда по любой из четных гармоник будет:

                                     S_2n=                                                                       (4-42)

Коэффициент  нетрудно вычислить, если известна зависи­мость В(H) или (H). Аппроксимируя зависимость (H) ломаной линией П-образной формы, показанной на рис. 4-22 штриховой ли-нией, получаем: =sin 2nθ, где m =  = µ* = 1/N (при Nµ1, см. § 4-3); θ= arcsin  и H_s – напряженность поля насыщения. Так как угол θ, в свою очередь, зависит от амплитуды H_m, то при заданном значении H_s всегда можно выбрать такой режим работы, когда |sin 2nθ| = 1. Следовательно, предельное значение чувствительности феррозонда по любой четной гармонике э. д. с. будет: S_2nмаск=8ω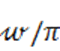. Это выражение может быть использовано для сравнения феррозондов с преобразователями других типов и при-кидочных расчетов.

Обычно используют вторую гармонику выходной э. д. с. феррозонда. Для второй гармоники проницаемости получаем: = 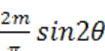. Поскольку

sin 2θ = 2 sin θ cos θ = ,

то чувствительность феррозонда по второй гармонике э. д. с. будет:

S₂=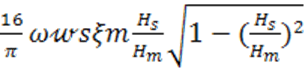.                                          (4-43)

Формула (4-43) позволяет вычислить чувствительность феррозонда при любом значении амплитуды напряженности Н_m поля возбуждения.

В формулу (4-43) введен коэффициент ξ, причем ξ = ξ₁ ξ₂ ξ₃, где ξ₁ = 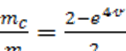; m_c - проницаемость системы из двух сердечников и = 2δ[ln kl/(δ+h)-1], см. § 4-3;

ξ ₂= ,

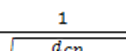d_cp – средний диаметр измерительной обмотки и ξ₃ — коэффициент, учитывающий потери за счет электропроводности сердечников. Общий коэффициент ξ обычно близок к 0,5 [4-40].

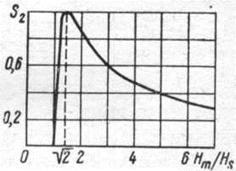
Рис. 4-23. Зависимость чувствительности ферро­зонда с продольным возбуждением от амплитуды поля возбуждения

Зависимость S₂(Н_m) нетрудно получить из (4-43). Она показана на рис. 4-23. Эта зависимость может быть получена и экспериментально, для чего при B_i = const измеряют амплитуду ε₂ как функцию Н_m. Опыт показывает, что измеренные таким образом зависимости хорошо согласуются с расчетными.

Значением Н_m обычно задаются исходя из обеспечения устойчивой работы феррозонда и низкого уровня шумов (см. § 4-12).

Расчеты, проводимые по формуле (4-43), хорошо совпадают с экс­периментом для значений m = 500  3000. Для больших значений m формула дает завышенные результаты, что объясняется погрешностями аппроксимации зависимости (H) ломаной линией П-образной формы. Вопросам более точной аппроксимации зависимостей В(Н) и (H) конкретных материалов посвящена работа [4-48].

4-11. Феррозонды с поперечным возбуждением

Феррозонд с поперечным возбуждением, работающий во втором режиме, был впервые предложен в Советском Союзе группой сотруд­ников Горьковского физико-технического института во главе с Г. С. Гореликом [4-49, 4-50].

Конструкция феррозонда горьковчан чрезвычайно проста (рис. 4-24, а). В качестве сердечника использована пермаллоевая проволока, по которой протекает переменный ток, создающий цирку­лярное (поперечное к продольной оси проволоки) магнитное поле, периодически намагничивающее проволоку. В направлении про­дольной оси проволоки нанесена измерительная обмотка, в которой при наличии внешнего поля B_i наводится полезная э. д. с.

Ретроспективно, главным образом в свете исследований Горелика [4-49], можно указать также на работы Гаррисона  [4-40].

Модификации феррозондов с поперечным возбуждением, являющиеся развитием феррозонда горьковчан, показаны на рис. 4-24, б, в, г. В этих конструкциях взамен проволочных сердечников использованы трубчатые, которые: 1) не разогреваются током возбуждения, так как последний протекает по тороидальной обмотке либо по осевому проводу; 2) равномерно промагничиваются по толщине во всем объеме (из-за малых толщин трубок); 3) обладают необходимой жесткостью. Подобные феррозонды описаны в работах [4-51 - 4-56]. На низких (звуковых) частотах возбуждения ω = 2π (10³10⁴) наиболее целесообразной конструкцией феррозонда является показанная на рис. 4-24, б.

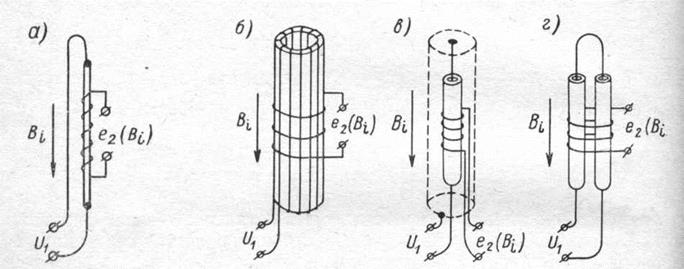
Рис. 4-24. Феррозонды с поперечным возбуждением: проволочный (а), трубчатый (б), коаксиальный (в)и дифференциальный (г)

Оценим чувствительность феррозонда с поперечным возбуждением. Прежде всего отметим, что при исследовании работы феррозондов с поперечным возбуждением продольная компонента индукции не может быть представлена в виде ряда (4-37).

Если напряженность измеряемого поля Н_|| = B_i/µ₀ мала, то В_|| =µ₀µ*Н_||, где µ* - нормальная проницаемость сердечника. Очевидно, что при наложении поперечного поля  и при H_|| = const нормальная проницаемость µ* может измениться только за счет воздействия поля , т. е. можно записать: В_|| (H_||, ) = µ₀µ* () H_||. Пусть (t) = Н_т sin ωt, тогда при Н_т = const имеем: В_|| (t) = µ₀µ* (t) H_||, откуда э. д. с. в измерительной обмотке

e = -.                                       (4-44)

Выражение (4-44) аналогично выражению (4-39). Различие между ними состоит лишь в том, что в (4-39) используется дифференциальная проницаемость а в (4-44) – нормальная µ^*

Поскольку зависимость µ^* (H) — четная, то по аналогии с (4-40) имеем:

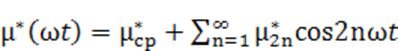                                                                      (4-45)

Учитывая плавный характер зависимости (H), функцию µ^*(ωt) в первом приближении можно аппроксимировать косинусоидой. Тогда взамен (4-45) получим

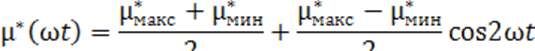
Отсюда с учетом (4-44) находим

S2 = .     (4-46)

Для случая µ_макс = m, µ_макс  µ_мин принимая во внимание что µ_мин = B_s/µ₀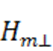 и B_s = µ₀µ_макс где — поле насыщения, получаем из (4-46):

S₂ = 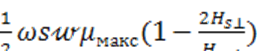.                           (4-47)