Магнитометрические преобразователи, приборы, установки, страница 8

Очевидно рассматриваемый тип механического преобразователя может быть использован не только для измерения составляющих, но и для измерения модуля магнитной индукции В₀. В этом случае магнит необходимо установить так, чтобы его магнитная ось и ось вращения были перпендикулярны направлению вектора В₀.

3. В магнитное поле помещен астатический преобразователь, со­стоящий из двух магнитных стрелок, подвешенных на одной и той же упругой нити на расстоянии ∆i. Пусть вектор магнитной индукции В₀ изменяется в пространстве как по модулю, так и по направлению. Тогда на нижнюю стрелку будет действовать вращающий момент Р'=Мsinθ-Мsin(90°-θ), а на верхнюю — момент P"=-sinθ+Msin(90°-θ), где , , , — проекция векторов  и  на координатные оси х и у. (рис. 3-8).

Суммарный вращающий момент, действующий на астатический преобразователь равен: P_∑= Р'+Р"= М(-)sinθ - М(-) cosθ = М∆igrad_z sinθ -

- М∆i grad_z B_oy cosθ, где grad_z  и grad_z B_oy – гра­диенты составляющих B_ox и B_oy по направлению z. Приравняв момент P_∑ к противодействую­щему моменту Р_пр = сφ, полу­чим

φ=  (∆i M grad_z В_0х sin θ - M∆igrad_zB_oycosθ).                     (3-4)

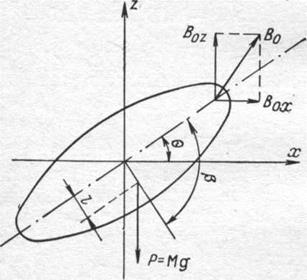
Рис. 3-7. К выводу условия равновесия в магнитном поле механического преобразователя на растянутых нитях

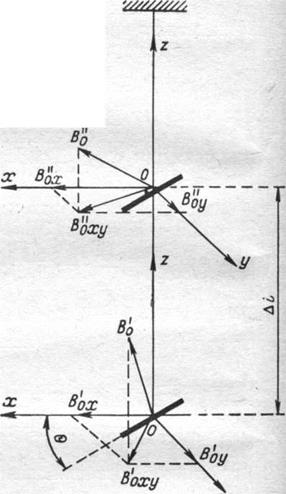
Рис.3-8. Астатический преобразователь в неоднородном магнитном поле

4. Рассмотрим теперь действие на магнитную стрелку магнитного поля, изменяющегося во времени по периодическому закону. Будем считать, что стрелка расположена в горизонтальной плоскости и мо­жет совершать лишь вращательные движения вокруг вертикальной оси. Движение стрелки в общем случае описывается известным урав­нением

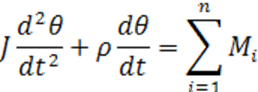
где J - момент инерции подвижной части преобразователя; - коэффициент торможения,  - сумма всех моментов, действующих на подвижную часть преобразователя.

Поскольку механические преобразователи для измерения магнит­ной индукции переменных полей применяются крайне редко (в основ­ном в приборах, предназначенных для измерения вариаций магнит­ного поля Земли), то практический интерес представляет рассмотре­ние только частного случая, когда на магнитную стрелку действуют одновременно постоянное поле с магнитной индукцией В₀ и пере­менное с амплитудой δВ₀, причем δВ₀  В₀. В этом случае суммар­ный момент

,                        (3-6)

где φ — угол, на который закручена нить;  — угол между маг­нитной осью стрелки и направлением вектора В₀; θ – изменение этого угла под действием δВ₀; ω – частота переменной составляющей магнитного поля. Подставляя (3-6) в (3-5), получим

.

Так как δВ₀  В₀, то после разложения sin (θ₀ + θ) можно по­ложить sinθ  θ, a cosθ = 1. Тогда последнее уравнение при­водится к виду:

где 2h = p/J,  = (с + МВ₀ cosθ)/J.

Решение полученного уравнения известно:

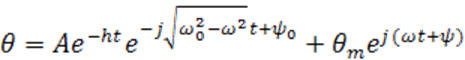,                   (3-7)

где

Первый член уравнения (3-7) представляет собой собственные ко­лебания магнита, которые при достаточно большом h быстро зату­хают, второй член — вынужденные колебания с амплитудой  и начальной фазой .  При ω₀ω

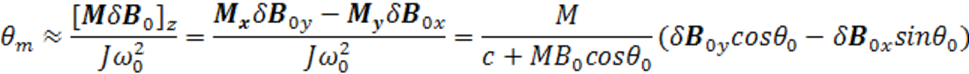
где , , М_х и М_у — составляющие переменной магнитной индук­ции и магнитного момента по осям х и у. Сомножитель в скобках правой части выражения (3-8) — есть проекция вектора  на направление, перпендикулярное магнитному моменту магнита М. Обозначим ее . Тогда

                                                                     (3-9)

Таким образом, при ω₀  ω магнитометр будет без искажения регистрировать а коэффициент S будет являться чувствитель­ностью механического преобразователя к магнитной индукции в пере­менном поле.

Так как трудно изготовить механический преобразователь с соб­ственной частотой колебаний больше нескольких герц, то измерение магнитной индукции переменных полей с помощью механических преобразователей производится только в тех случаях, когда частота со не превышает указанной величины.

Чувствительность механических преобразователей к магнитной индукции постоянного поля сравнительно велика и, как мы увидим во второй части книги, позволяет создавать приборы для измерения магнитной индукции с порогом чувствительности порядка единиц нанатесла и меньше.

Порог чувствительности механических преобразователей в ряде случаев определяется нестабильностью нулевого сигнала (погреш­ностью нуля), под которой подразумевают нестабильность началь­ного угла между магнитной осью преобразователя и соответствующей координатной осью. Случайная составляющая погрешности нуля (аддитивный шум) объясняется наличием тряски и воздушных пото­ков, возникающих вследствие градиента температуры и воздействую­щих на магнитную стрелку. С целью уменьшения этих погрешностей механический преобразователь устанавливают на массивном фунда­менте и помещают в домик — специальный ящик, одна или две про­тивоположные стенки которого выполняются из стекла. Воздух из домика часто откачивается. Герметизация особенно необходима, если магнит сделан из викаллоя. Викаллоевый магнит после его термо­обработки покрывается окалиной, которая хорошо впитывает влагу, что приводит к появлению систематической погрешности.

3-5. Использование механических преобразователей для абсолютного и относительного измерения магнитной индукции

Одно из основных достоинств механических преобразователей со­стоит в возможности использования их для абсолютного измерения модуля В0. Впервые абсолютный метод измерения магнитной индук­ции был предложен Гауссом [3-5]. Метод Гаусса основан на законах взаимодействия между постоянными магнитами и магнитным полем и заключается в непосредственных измерениях периода качания в горизонтальной плоскости магнита, помещенного в измеряемое поле, и наблюдении угла отклонения другого магнита, вызываемого первым магнитом. Положения, в которых находятся оба магнита (стрелки ns и отклоняющий магнит NS) относительно друг друга, принципиально могут быть любыми, однако для упрощения расчета обычно используют одно из четырех положений, два из которых пред­ложены Гауссом, а два Ламоном (рис. 3-9).

Можно показать [3-6], что соотношения между магнитной индук­цией и углом отклонения стрелки 6 имеют вид: для первого гауссова положения

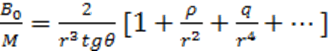                                              ;                                  (3-10)