Магнитометрические преобразователи, приборы, установки, страница 6

Если магнитное поле В₁ вращается синхронно с прецессией, то возникает дополнительный момент, стремящийся увеличить угол α между µ и В. В результате происходит изменение ориентации µ, сопровождающееся переходом ядра с одного уровня на другой. Если же ω₁ — скорость вращения В₁ — отлична от скорости пре­цессии ω₀, то действие будет периодически изменять свой знак с раз­ностной частотой ω₁-ω₀, оставаясь в среднем (для достаточно боль­шого промежутка времени), равным нулю. Эти же рассуждения спра­ведливы для случая, когда ω₁=ω₀, но направление вращения В₁ противоположно направлению прецессии.

Таким образом, эффект взаимодействия наступает лишь при усло­вии совпадения по величине и направлению ω₁ и ω₀, т. е. носит резко выраженный резонансный характер. Так как ω₀= 2πf, но ω₀= = γВ, то становится ясно, что классическое условие резонанса точно совпадает с квантовомеханическим условием, определяемым выра­жением (1-21).

Помимо перечисленных выше, известен еще целый ряд физических явлений и эффектов, связанных с различными проявлениями магнит­ного поля: эффекты Фарадея, Керра, Коттона—Мутона, Джозеф-сона и др.

Эффект Фарадея состоит в том, что при прохождении плоскополяризованного света в магнитном поле, направленном вдоль светового пучка, плоскость поляризации последнего поворачивается на угол α = υB₀l, где υ — постоянная Верде; l — часть длины светового луча, находящегося в магнитном поле. Эффект Фарадея практически безынерционен и характеризуется временем порядка 10^-10 сек. Эффект Фарадея иногда используется при плазменной диагностике [1-6].

Экваториальный эффект Керра заключается в том, что при отра­жении света от периодически намагничиваемой ферромагнитной пленки периодически изменяется интенсивность отраженного света пропорционально намагниченности образца [1-7]. Достоинство эф­фекта состоит в возможности создания миниатюрных С преобразователей размером 10^-13 см³ и проведении измерения на расстоянии.

С эффектом Керра во многом схож эффект Коттона—Мутона, за­ключающийся в двойном лучепреломлении поля. При этом оптиче­ской осью является направление магнитного поля. Разность показа­телей преломления для обыкновенного и необыкновенного лучей в направлении, перпендикулярном к оптической оси, зависит от магнитной индукции n₂ - n₂ = kB₀. Вели­чина D=k/λ называется постоянной Коттона—Мутона, она зависит от дисперсии λ и свойств жидкости.

Открытие эффектов Джозефсона про­изошло после того, как в 1961 г. Ф. Лондон выдвинул идею о существова­нии кванта магнитного потока, которая и была вскоре подтверждена эксперимен­тально. С помощью эффектов Джозефсона, в том числе эффекта туннелирования тон­кого изоляционного барьера связанными электронными парами сверхпроводника, стало возможным наблюдение единичных квантов магнитного потока Ф₀ = h/2e₀ [1-8], где Ф₀ — квант магнитного потока, равный 2,07-10^-15 вб; е₀ — заряд электрона. 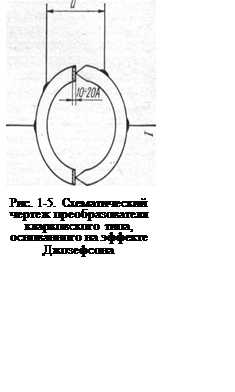Если кольцо из мате­риала в сверхпроводящем состоянии (слабая сверхпроводимость) имеет две слабых связи — узлы Джозефсона (рис. 1-5), например две проволочки или полоски из тантала, ниобия или сплава PbSn при температуре в несколько граду­сов Кельвина разделены тонким слоем диэлектрика — окисла металла тол­щиной 1020, то при прохожде­нии через узлы тока I, большего, чем некоторый ток I_m (ток Джозефсона), слабая сверхпроводимость раз­рушается, и на переходе появляется 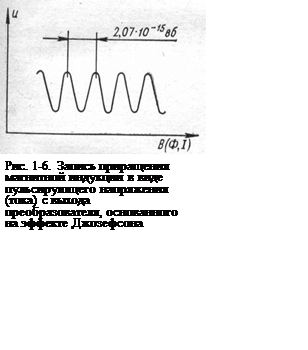падение напряжения и. При пере­ходе пары электронов барьера с по­тенциалом дополнительная энергия, приобретаемая электроном, излу­чается (поглощается) в виде фотонов с энергией hω₀ = 2eu, т. е. через переход течет ток высокой частоты i= I_m sin ωt (так называемый нестационарный эффект Джозефсона) и некоторый постоянный ток. На рис. 1-6 показана типичная запись постоянного тока, определяющего измеряемый магнитный поток или индукцию. Один период проходящего переменного тока равен кванту магнитного потока Ф₀. Отсчитывая число периодов переменного тока, можно тем самым определить приращение маг­нитного потока (или индукции) в охватываемом сверхпроводящим кольцом сечении.

1-4. Возможные классификации магнитометрических преобразователей

В основу наиболее распространенной классификации магнитометрических преобразователей положено деление по принципу использования в них того или иного физического явления (эффекта). Большое число этих явлений, а следовательно, и различных типов преобразователей, свидетельствует о разносторонней и всеобъем­лющей природе магнетизма.

Классификация по принципу используемого физического явления способствует обстоятельному описанию и изучению каждого типа преобразователя. В настоящее время уже невозможно сделать следующий шаг в развитии магнитометрической тех­ники, не будучи специалистом какой-либо конкретной отрасли физических знаний. Разработка индукционных преобразователей активного типа базируется сейчас не только на знаниях электротехники, но и на изучении магнитных, диэлектриче­ских и упругих свойств твердого тела. Развитие гальваномагнитных преобразовате­лей тесно связано с физикой полупроводников и технологией изготовления новых материалов. Освоение и совершенствование радиооптических преобразователей не­мыслимо без изучения квантовой механики и оптики.

Таким образом, классификация преобразователей по принципу используемого физического явления является основной и наиболее действенной классификацией. Она и положена в основу написания первой части книги, посвященной магнитометри­ческим преобразователям.

Наряду с классификацией по принципу используемого физического явления, акцентирующей внимание на конкретных особенностях каждого типа преобразова­теля, очевидно, должна существовать и иная классификация, позволяющая сравни­вать различные типы преобразователей между собой. Такую классификацию можно осуществить на основе деления преобразователей, а затем и приборов по роду изме­ряемой величины.

Величиной, непосредственно воздействующей на преобразователь, является, как уже отмечалось, вектор магнитной индукции В. В тех случаях, когда направле­ние вектора В неизменно или когда можно пренебречь изменениями этого направле­ния достаточно измерять скалярное значение магнитной индукции, т. е. величину В. Величины В и В могут быть функциями времени; при этом они остаются, соответ­ственно, скалярной и векторной величинами. Если величины В и В оказываются функциями координат, то возникает необходимость в измерении градиента или -тен­зора, характеризующих неоднородность магнитного поля и его структуру.