Поскольку силовой и электромагнитный эффекты, наблюдаемые в намагничиваемых средах, оказываются пропорциональными вектору В, то измеряемой, точнее преобразуемой в результате проявления указанных эффектов величиной следует считать вектор В, а вне намагничиваемых сред вектор В0, а не Н. Измерительные преобразователи или приборы можно при этом отградуировать в одних и тех же единицах независимо от того, в каких средах (намагничиваемых или ненамагничиваемых) будут производиться измерения.
1-2. Уравнения Максвелла. Пространственные и временные характеристики магнитного поля
Экспериментально установленные законы электромагнетизма были обобщены Максвеллом, который получил уравнения, справедливые для неподвижных сред:
rot H = j+![]() , (1-2)
, (1-2)
rot E = -![]() , (1-3)
, (1-3)
div B = 0, (1-4)
div D = ρ. (1-5)
Здесь D — электрическая индукция; j — плотность тока проводимости и переноса; ρ — плотность электрических зарядов.
Интегрируя уравнения (1-2) и (1-3) по поверхности и используя теорему Стокса, можно получить закон электромагнитной индукции и закон полного тока. Из уравнения (1-3) имеем:
![]() .
.
Аналогично из (1-2): ![]() =
=![]() = l∑где l∑ - суммарный ток, складывающийся из токов проводимости,
переноса и тока смещения; е — электродвижущая сила.
= l∑где l∑ - суммарный ток, складывающийся из токов проводимости,
переноса и тока смещения; е — электродвижущая сила.
Для стационарного случая, когда dD/dt =0, т. е. для случая постоянных токов: rot Н = j, div В = 0.
Решение этих уравнений, как правило, сопряжено со значительными трудностями. Поэтому часто в целях упрощения расчетов вводится вспомогательная векторная функция А, называемая векторным потенциалом и определяемая из условия rot А = Н.
Наложение этого условия
оказывается возможным, поскольку дивергенция ротора любого вектора тождественно
равна нулю, т. е. всегда справедливо (1-4). Из множества векторных функций,
удовлетворяющих уравнению rot А = Н, выбирается такая функция, для которой выполняется
равенство div А = 0. Тогда в случае изотропных сред (при ![]() = const) получим ∆А = j, где ∆ =
= const) получим ∆А = j, где ∆ = ![]() 2;
2;
![]() = х0
= х0 ![]() – оператор Гамильтона. Решение последнего уравнения
имеет вид:
– оператор Гамильтона. Решение последнего уравнения
имеет вид:
A = ![]() ,
,
где r — расстояние от элемента объема dυ до точки, в которой вычисляется вектор Н.
Применив к вектору А операцию ротации, т.е. дифференцирования по координатам точек, в которых вычисляется вектор векторного потенциала А, найдем
H = ![]() ,
,
Полученное выражение представляет собой еще одну форму записи закона Био—Савара.
В пространстве, где нет токов, rot Н = 0. В этом случае оказывается удобным ввести некоторую вспомогательную функцию φм, называемую магнитным потенциалом и связанную с напряженностью магнитного поля соотношением
Н = -grad φм = -![]() φм.
φм.
Как векторный, так и скалярный (магнитный) потенциалы являются лишь удобными расчетными величинами и, как правило, непосредственно не измеряются. Указанными величинами широко пользуются, например, при расчете полей, создаваемых катушками в частности служащими для воспроизведения определенных значений магнитной индукции.
Пользуясь декартовой или сферической системой координат, вектор В можно представить в виде В = f (Вх, Вуу Вг) или В = f (ψ, θ, B), где
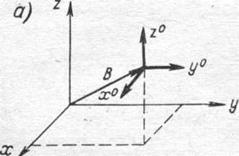
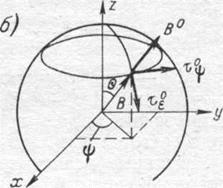
Рис. 1-1. Декартова (а) и сферическая (б) системы координат
Вx, Ву, Вz — проекции вектора В на оси декартовой системы координат; ψ, θ — углы, определяющие положение вектора В в сферической системе координат; В — модуль вектора (рис. 1-1, а и б).
 В тех случаях, когда
направление вектора В при переходе от одной точки к другой остается
неизменным или когда можно пренебречь изменением направления вектора В, пользуются модулем В. Неоднородность поля в этом
случае характеризуется градиентом
В тех случаях, когда
направление вектора В при переходе от одной точки к другой остается
неизменным или когда можно пренебречь изменением направления вектора В, пользуются модулем В. Неоднородность поля в этом
случае характеризуется градиентом ![]() В = х0дВ/дх + у0дВ/ду + z0дВ/дг. Здесь х0, у0, z0 — орты декартовой системы координат; дВ/дх, дВ/ду, дВ/дz — проекции вектора
В = х0дВ/дх + у0дВ/ду + z0дВ/дг. Здесь х0, у0, z0 — орты декартовой системы координат; дВ/дх, дВ/ду, дВ/дz — проекции вектора ![]() В на соответствующие оси.
В на соответствующие оси.
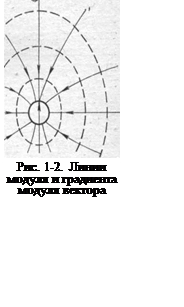
По аналогии с линиями магнитной индукции и напряженности поля можно пользоваться также и линиями градиента модуля магнитной индукции. Эти линии всегда направлены в сторону источника поля, намагниченного тела или контура с током (рис. 1-2).
Если изменением направления вектора В при переходе от одной точки к другой пренебречь нельзя, то неоднородность поля по заданному i-му направлению характеризуется величиной
∂B/∂i =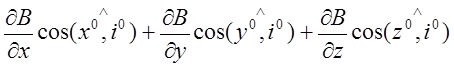 .
(1 -6)
.
(1 -6)
В свою очередь, величины дB/дх, дВ/ду, дВ/дz могут быть представлены в виде:
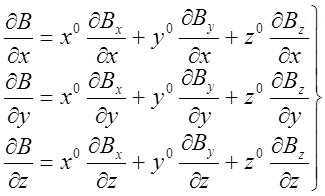
либо в виде:
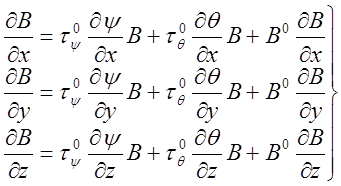
где ![]()
![]() и В0 — орты сферической системы
координат (рис. 1-1, б).
и В0 — орты сферической системы
координат (рис. 1-1, б).
Из выражений (1-6)—(1-8)
следует, что для определения ∂B/∂i необходимо задать девять величин. Другими словами,
неоднородность поля вектора В в i-м направлении выражается через
некий тензор. Указанные девять величин, характеризующие неоднородность вектора
В, несут большую информацию о
поле, чем три величины, характеризующие градиент модуля В. Это наглядно видно из
уравнений (1-8), где величины дВ/дх, дВ/ду и dB/dz, определяющие градиент ![]() В,
входят лишь в последний столбец системы.
В,
входят лишь в последний столбец системы.
Величины, входящие в уравнения (1-7) и (1-8), являются слагаемыми дивергенции и ротора.
Определяя производные вектора В по трем направлениям, совпадающим с ортами выбранной системы координат, мы получаем, таким образом, возможность судить о том, где находится источник магнитного поля (токовая система). Последнее особенно ценно при исследовании процессов в проводящих средах (морской воде, плазме и т. д.). Магнитное поле может изменяться также и во времени.
Вектор-функцию В (t) удобно записать в виде В (t) = В (t) В0 (t), где В0 (t) — единичная вектор-функция, определяющая в каждый момент времени направление вектора В.
Временная характеристика магнитного поля может обусловливаться, следовательно, как изменением модуля В, так и изменением направления В0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.