Учебное пособие по курсу "Теория механизмов и машин", страница 49

На рис. 8.4, где приведен образец диаграммы моментов, проиллюстрирован метод графического интегрирования. Ординаты равновеликих прямоугольников М_п.0-1, М_п.1-2 и т.д. приблизительно соответствуют средним значениям моментов, угловой шаг Δφ.

Выбирают полюс интегрирования Р₁ на отрезке интегрирования Н₁. При выполнении курсового проекта рекомендуется принимать Н₁ = 40…60 мм. Полюс интегрирования соединяют прямой (лучом) с точкой пересечения четвертой стороны равновеликого прямоугольника с осью ординат. На первом участке диаграммы работ из начала координат проводят отрезок, параллельный первому лучу.

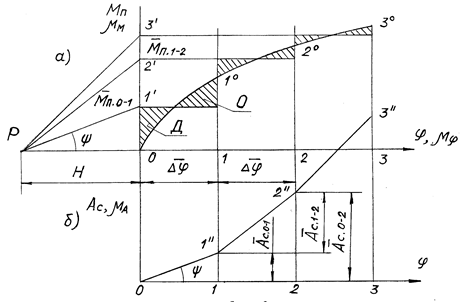
Рис. 8.4

Доказывается, что ордината 1–1″ на рис. 8.4, б является графическим изображением работы сил сопротивления  на участке 0–1. Из треугольника Р–0–1¢  следует:

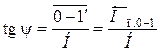                                    .                          (8.10)

Из Δ 0–1–1″:

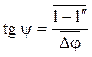                                          .                                (8.11)

Приравнивая правые части уравнений (8.10) и (8.11) и учитывая, что работа А = МΔφ, получают:

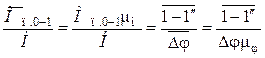                         ,                        откуда

                  .        (8.12)

Таким образом, отрезок, параллельный лучу, проведенному из полюса интегрирования в точку пересечения четвертой стороны равновеликого прямоугольника с осью ординат, изображает в узловой точке работу сил сопротивления на выбранном участке. Масштаб диаграммы работ в мм/Дж в соответствии с формулой (8.12):

                                        μ_А = μ_м μ_φ / Н₁.                               (8.13)

На втором участке из конца первого отрезка проводят отрезок, параллельный второму лучу, и т.д. На последнем из 12 участков ордината не будет равна нулю. Полученная ломаная линия приближенно представляет собой диаграмму А_с = А_с(j) — кривая III (рис. 8.3, в). Расстояние в направлении оси ординат между соседними узловыми точками диаграммы изображает приращение работы на участке, а расстояние между начальной и текущей точками — работу за временной отрезок, равный нескольким участкам.

NB 8.4. Порядок графического интегрирования.

1. Фигуры на подынтегральной диаграмме заменяют равновеликими прямоугольниками.

2. Четвертые стороны прямоугольников проводят до оси ординат.

3. Из полюса интегрирования в точки на оси ординат проводят лучи.

4. На первом участке интегрального графика проводят отрезок, паралельный первому лучу. Второй отрезок проводят из конца первого и т.д.

Величину работы сил полезного сопротивления за цикл определяют величиной ординаты в мм, соответствующей концу последнего участка, деленной на масштаб m_А.

8.4. Численное интегрирование

Этот прием применяют в тех случаях, когда функцию нельзя проинтегрировать в аналитической форме или это связано с большим объемом работы. Численное интегрирование ведут по квадратурным формулам Ньютона-Котеса, например, по правилам трапеций. В общем виде по правилам трапеций для n = 1 интеграл I запишется так:

                                        .                              (8.14)

По правилу Римисона для n = 2:

                                   .                         (8.15)

По правилу Уэддля для n = 6:

                  .        (8.16)

В формулах (8.14) – (8.16): Δx — размер участка по оси абсцисс; у₀, у₁, …у₆ — значения подынтегральной функции для заданных равноотстоящих точек.

Выражение (8.14) по сути представляет собой произведение среднего значения функции у на шаг Δx. Это соответствует определению интеграла как площади фигуры под графиком функции. Такой площадью на участке 0–1 (рис. 8.4, а) является площадь криволинейного треугольника 0–1–1⁰ либо произведение значения М_п.0-1 на шаг Δφ. Так, интеграл на участке 0–1 дает работу на участке 0–1:

                              А_0-1 = I₁ = 0,5 (М_п0 + М_п1) Δφ.                    (8.17)

Приращение работы на участке 1–2 определяется интегралом I₂:

                               I₂ = А_1-2 = 0,5(М_п2 + М_п3)Δφ.                            

Полная работа на участках 0–1 и 1–2 определяется суммой аналогично рис. 8.4: