Учебное пособие по курсу "Теория механизмов и машин", страница 15

В кривошипно-ползунном механизме (рис. 4.1, а) число степеней свободы W = 3n – 2p₁ = 3·3 – 2·4 = 1. В процессе структурного анализа, который предшествует кинематическому анализу, отсоединяют одну диаду 2-го вида (В–С), где неизвестной является кинематика средней точки С.

Из теоремы сложения скоростей известно, что абсолютная скорость точки твердого тела равна геометрической сумме скоростей переносного и относительного движений:

                                          ,                                  (4.9)

где  — абсолютная скорость;  — переносная скорость;  — относительная скорость.

В диаде 2–3 (рис. 4.1, а) известна кинематика точки В. Это означает, что при заданных угловой скорости w₁ и длине кривошипа l_AB, совершающего равномерное вращательное движение, можно определить линейную скорость _B и линейное ускорение a_B, которые будут неизменными в любом положении кривошипа. Также известно, что при равномерном вращении угловое ускорение кривошипа e₁ = 0 и _x–x = 0, так как направляющая x–x неподвижна. Неизвестна кинематика точки С. В ее движении относительно точки В векторное уравнение (4.9) записывают так:

                                         ,                               (4.10)

                                                ^AB ^CB,                                       где _B — переносная скорость, м/с; направлена перпендикулярно к звену 1 в сторону вращения:

                                                                            (4.11)

_CB — относительная скорость вращательного движения точки С относительно точки В; вектор скорости направлен перпендикулярно к звену 2 и прикладывается в точке С.

В уравнении (4.10) двумя чертами показан вектор, известный по величине и направлению, одной чертой — известный только по направлению. Следует обратить внимание на то, что в соответствии с уравнением (4.10) вращается точка С, а точка В принята за условный центр вращения. Скорость точки С также зависит от направляющей x–x. Второе уравнение:

                                                                     (4.12)

                                                 = 0    || x–x                                     

Уравнения (4.10) и (4.12) записывают совместно и решают как систему векторных уравнений:

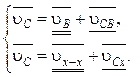                                                                  (4.13)

NB 4.7. Для построения плана скоростей систему векторных уравнений составляют для группы Ассура, где неизвестной является кинематика средней кинематической пары.

Решение системы (4.13) выполняют путем построения векторного многоугольника, называемого планом скоростей. Для этого из полюса p проводят вектор  перпендикулярно звену AB в сторону вращения. Масштаб плана скоростей, мм/(м∙с^-1):

                                            m_u = pb/u_B.                                  (4.14)

В соответствии с уравнением (4.10) из конца вектора  проводят направление _CB перпендикулярно звену СВ (рис. 4.1, б). В уравнении (4.12) первое слагаемое равно 0 и находится в полюсе p. Из полюса проводят направление _Cx параллельно x–x до пересечения с направлением _CB в точке С. В соответствии с векторными уравнениями искомые векторы направляют в искомую точку.

NВ 4.8. Свойства плана скоростей:

1) векторы, проведенные из полюса плана, изображают абсолютные скорости точек механизма; векторы, через полюс не проходящие, изображают относительные скорости для данного положения механизма;

2) свойство подобия планов: каждой точке плана положений соответствует точка на плане скоростей; фигуры на планах положений и скоростей геометрически подобны;

3) мгновенный центр вращения шатуна 2 находят на пересечении направления кривошипа АВ c перпендикуляром к направляющей x–x, восстановленном в точке С;

NB 4.9.

1) Векторы линейных скоростей направлены перпендикулярно звеньям в сторону вращения или параллельно направляющим;

2) Искомые векторы направляют в искомую точку.

NВ 4.10. Для определения величины скорости длину отрезка на плане делят на масштаб.

Искомая абсолютная скорость точки С: