Машиностроение \ Основы резания металлов

Теоретическое определение параметров процесса резания ширина и толщина среза при несвободном резании. Теоретический метод определения обрабатываемости материалов резанием, страница 8

Формулы (54), (60) и (61) получены при рассмотрении квазистационарного действия быстродвижущегося полосового источника тепла АВ постоянной интенсивности (см. рис. 10), расположенного под углом  к адиабатической поверхности. Тепловые источники при резании имеют объемный характер, так как пластические деформации металла протекают в определенных объемах зоны резания [10. 38, 66]. В данной работе рассмотрено также действие объемного ABON источника тепла (рис. 12), когда в условной плоскости сдвига АВ интенсивность тепловыделения является постоянной, а в направлении оси х, изменяющейся по экспоненциальному закону

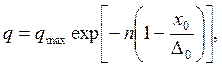                                    (63)

где qmax — максимальная интенсивность тепловыделения объемного источника в условной плоскости сдвига АВ; n = 3...5.


 


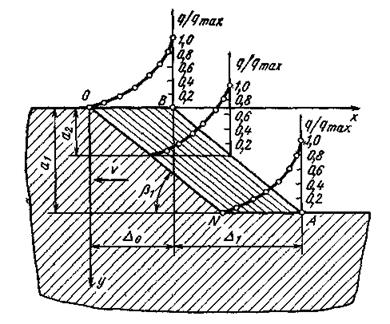
Рис   12   Схема действия полосового и объемного источников тепла в зоне первичных пластических деформаций обрабатываемого материала

Установлено, что при действии плоского и объемного наклонных источников тепла, расположенных под углом  максимальная температура развивается в точке А. Отношение максимальных температур  и  развивающихся соответственна при действии объемного и плоского источников тепла, определяется выражением

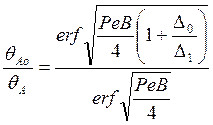                                  (64)

где   и — размеры источников.

Таблица   2

Отношение максимальных температур первичных пластических деформаций при действии объемного и плоского источников тепла, расположенных под углом

Величина отношения температур  при различных значениях PeB

1

5

10

20

0,1

0,5

1

2

1,045

1,18

1,31

1,50

1,02

1,07

1,10

1,12

1,005

1,02

1,025

1,025

1,00

1,00

1,00

1,00

 


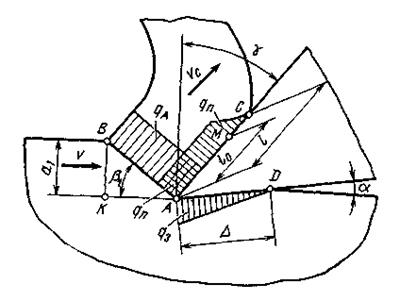Рис.   13.  Схемы   распределения   суммарных интенсивностей   тепловыделения   в   плоскости  сдвига  и  на  контактных  поверхностях инструмента

Количественный анализ выражения (64) показал, что влияние объемности источника на отношение максимальных температур уменьшается с увеличением РеВ и уменьшением отношения  (табл. 2). При всех значениях  влияние объемности источника можно практически не учитывать при  объемный источник как бы «перерождается» в плоский.

СУММАРНЫЕ ИНТЕНСИВНОСТИ ТЕПЛОВЫДЕЛЕНИЯ (УДЕЛЬНЫЕ     ТЕПЛОВЫЕ ПОТОКИ) ПРИ РЕЗАНИИ МАТЕРИАЛОВ

Процессы резания характеризуются наличием трех основных быстродвижущихся по отношению к стружке и детали плоских источников тепла шириной b1 и длиной 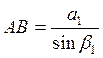  АС = l и AD = (рис. 13). Источники АС и AD по отношению к резцу являются неподвижными.

При анализе тепловых явлений при резании характер изменения интенсивностей тепловыделения на участках АВ, АС и AD можно принимать аналогичными характеру изменения касательных напряжений  на этих участках, так как последние определяют величину силы и работы трения.

Максимальные    интенсивности тепловыделения     (удельные тепловые потоки) qА, qп и qз определяем из уравнений баланса механической и тепловой энергий в условной плоскости сдвига АВ и на контактных площадках  AC=l  и AD=


Определение qA. Механическая энергия пластического деформирования материала в условной плоскости сдвига АВ и вблизи нее определяется выражением (55).

Выделившаяся за 1 с теплота

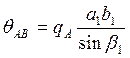   дж/с                                              (65)

Так как Lab = ab, то имеем

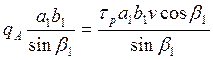
После сокращений получаем

                                                   (66)

Таким образом, интенсивность тепловыделения в условной плоскости сдвига АВ тем больше, чем прочнее обрабатываемый материал (р), выше скорость резания v и меньше угол наклона, условной плоскости сдвига (больше усадка стружки).

Определение   qп. Механическая энергия   трения на передней контактной площадке инструмента

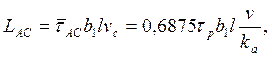                                           (67)

где — среднее касательное напряжение на участке   АС. Выделившаяся за 1 с теплота

                                     (68)

где  — средняя интенсивность    тепловыделения    на участке АС. Из равенства выражений (67) и (68) получаем

Скачать файл