Основы информатики и вычислительной техники: Учебно-практическое пособие, страница 9

Сигналы вида  обычно называют центрированными. Начальная моментная функция второго порядка (ν=2) характеризует математическое ожидание квадрата процесса, т.е. M[x²(t)], а центральная моментная функция второго порядка (ν=2)

                                               (1.10)

носит название дисперсии

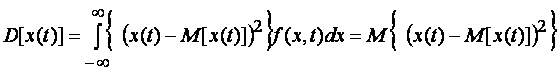    .   (1.11)

Корреляционной (автокорреляционной, автоковариационной) функцией называют математическое ожидание произведения

     .                                  (1.12)

Случайные сигналы принято разделять на нестационарные (статистические характеристики зависят от начала отсчета времени) и стационарные. Строго говоря, стационарные случайные сигналы, как и стационарные физические системы, не существуют. Однако, стационарные случайные сигналы являются очень «удобной» идеализацией и в практических задачах играют чрезвычайно большую роль. Стационарными случайные сигналы могут быть в «большей или меньшей степени»: в узком и широком смысле. Стационарность в узком смысле – полная стационарность; в этом случае все плотности вероятности значений случайного сигнала не зависят от положения начала отсчета, т.е. не зависят от одинакового временного сдвига t₀ всех точек t₁, t₂…t_n вдоль оси времени:

.

Стационарность в широком смысле предполагает, что на случайный сигнал накладывается наименьшие ограничения. Это сигнал, статистические характеристики которого не зависят от времени, – математическое ожидание постоянно, а корреляционная функция зависит только от аргумента , т.е.

.

В дальнейшем изложении, если не будет сделано специальных оговорок, речь будет идти о стационарных, в широком смысле, сигналах.

Среди стационарных случайных сигналов выделяют особую группу эргодических сигналов, которые подчиняются эргодическое теореме. Эта теорема гласит о том, что для эргодических сигналов результаты усреднения по множеству реализаций совпадают с их средними значениями на бесконечно большом интервале времени одной единственной реализации. Отсюда следует вывод о том, что для эргодических сигналов всегда можно выбрать такую конечную длину реализации, результаты усреднения по которой, совпадут с выборочной средней оценкой, полученной по заданному числу реализаций. Последнее положение особенно важно в области измерений статистических характеристик случайных сигналов, поскольку измерительная процедура и аппаратурная реализация различных алгоритмов в этом случае значительно упрощаются.

Для эргодических сигналов (далее, при отсутствии специальных оговорок, речь будет идти только о них) справедливы следующие определения.

Математическое ожидание определяется как среднее по времени

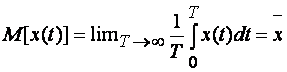    .                      (1.13)

Дисперсия (мощность)

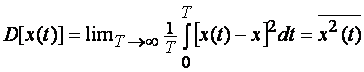                              (1.14)

Корреляционная функция

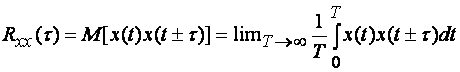           (1.15)

Для центрированных сигналов корреляционная функция:

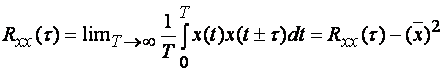               (1.16)

При аппаратурном определении числовых характеристик случайных сигналов часто пользуются приближенным значением – оценкой (здесь и далее для обозначения оценок используется знак «звездочка»):

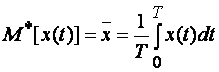                               (1.17)