Основы информатики и вычислительной техники: Учебно-практическое пособие, страница 8

m_n=M(ξ-а)^ν,                                          (1.3)

где М – обозначает операцию математического ожидания. Начальный момент первого порядка (ν=1) определяется относительно а = 0 и называется математическим ожиданием случайной величины ξ, т.е.  m₁=M(ξ)=a.

Центральный момент второго порядка (ν=2) определяется относительно центра распределения и называется дисперсией случайной величины ξ, т.е. D_ξ=M(ξ-a)².

Математическое ожидание и дисперсия дискретной случайной величины ξ определяются по формулам:

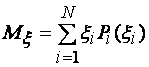                                    (1.4)

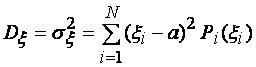                        (1.5)

В случае непрерывной величины ξ:

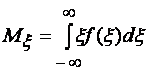                                    (1.6)

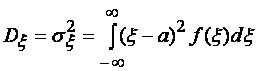,                    (1.7)

где  обозначает среднеквадратичное отклонение случайной величины.

Математическое ожидание M_ξ и дисперсия D_ξ являются функционалами, описывающими свойства распределения случайной величины ξ : M_ξ характеризует «средневзвешенное» положение величины ξ, а D_ξ  – ее рассеяние относительно математического ожидания.

Рассмотренные характеристики F_ξ(x,t_i) и f_ξ(x,t_i) являются одномерными, т.к. они получены при фиксированном значении аргумента t=t_i. Более полной характеристикой случайного сигнала х(t) является двумерный закон распределения f_ξ(x,t₁;x,t₂), заключающий в себе связь между значениями функции в два момента времени. Очевидно, что наиболее полной характеристикой случайного процесса мог бы служить только «бесконечномерный» (n-мерный) закон распределения (в силу непрерывности аргумента – времени) f(x,t₁;x,t₂;…x,t_n). Однако на практике существуют и лучше изучены некоторые типы случайных сигналов, свойства которых полностью определяются законом распределения при малом числе n (обычно для n < 3). К такому классу случайных сигналов относятся  чисто случайные сигналы, характеризующиеся независимостью значений х(t) в различные моменты времени (для таких сигналов f_ξ(x,t₁;x,t₂,…,x,t_n)= f_ξ(x,t₁)· f_x(x,t₂)·…f_ξ(x,t_n). Чисто случайный процесс является идеализацией, т.к. в реальных процессах всегда существует статистическая связь между значениями х(t) в достаточно близкие моменты времени. Другим примером являются марковские (по имени математика А.А. Маркова) случайные сигналы, для которых, в силу их безынерционности, любая n – мерная плотность вероятности их значений может быть получена из двумерной плотности вероятности.

Получение многомерной плотности вероятности в общем случае представляет собой весьма трудную задачу. Поэтому для многих практических областей применения при определении статистических характеристик случайного сигнала, как и случайной величины, вполне достаточно знания некоторых интегральных (усредненных) характеристик, но вместо моментов порядка ν в случае случайных величин, моментных функций различных порядков ν

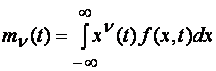                                (1.8)

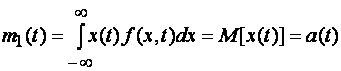При                             (1.9)

Эта функция времени называется математическим ожиданием случайного сигнала х(t). Очевидно, что математическое ожидание случайного сигнала представляет собой некоторую среднюю кривую, около которой располагаются его возможные реализации.