Основы информатики и вычислительной техники: Учебно-практическое пособие, страница 25

Табл. 1.3

Предположим, что вероятности всех возможных результатов выражаются числами

, где – целые положительные числа. причем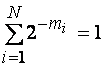

Из таблицы 1.3 видно, что если вероятность какого-либо события равна , то его двоичный номер (двоичное кодовое слово) выразится -значным двоичным числом.

При проведении опытов количество двоичных знаков в числе, соответствующем номеру опыта, будет случайной величиной с возможными средними значениями  и с вероятностями .

Естественно, за меру неопределенности H принять среднее арифметическое значение числа двоичных знаков необходимых, чтобы полностью определить общий результат, т.е. определить величину .

Среднее арифметическое значение случайной величины  равно

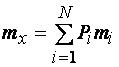
или

         (1.66)

В нашем примере

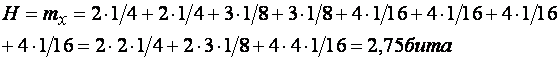
Это и есть математическое ожидание числа двоичных знаков на одно сообщение.

Если предположить, что вероятности всех восьми сообщений равны друг другу, т.е. каждое сообщение имеет одинаковое количество информации, то , что соответствует мере информации по Хартли  бита. Таким образом может иметь место экономия в числе передаваемых символов при одной и той же информации.

Понятие информации, как было показано выше, тесно связано с понятием неопределенности. Мера неопределенности есть непрерывная функция вероятностей состояний источника информации. Чем больше вероятность, не получая информацию, правильно угадать состояние системы, тем меньше неопределенность источника, и наоборот, чем меньше априорная вероятность события, тем большее количество информации оно несет, тем больше его неопределенность.

Например, имеются 2 источника (Табл. 1.4а и 1.4б)

                   а)                                                     б)

                                               Табл. 1.4

Ясно, что у 2-ого источника неопределенность меньше: он на 99% находится в состоянии Х₁; 1-ый источник с вероятностью 0,5 (или на 50%) находится в состоянии Х₁.

Таким образом сообщение несет полезную информацию тогда, когда имеется энтропия – неопределенность состояний источника сообщений. Если опыт имеет один исход, то получатель знает исход опыта заранее и не получает никакой информации (неопределенность отсутствует). Если опыт имеет два исхода – имеет место определенная информация и неопределенность. Чем меньше априори вероятность события, тем большее количество информации оно имеет.

Рассмотрим основные свойства энтропии.