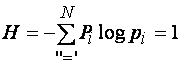 (1.66)
(1.66)
В общем случае в (1.66) неизвестных три: число возможных состояний N, вероятность Pi, и основание логарифма. Два из этих неизвестных можно задать, а третье получить из (1.66).
В простейшем случае N=2, а P1=P2=1/2, тогда
![]()
![]() Отсюда а=2.
Отсюда а=2.
Таким образом единицей измерения энтропии служит энтропия системы с двумя равновероятными состояниями, вычисленная с помощью логарифма, с основанием 2. Это двоичная единица энтропии - «бит».
В случае десятичной системы счисления (основание а=10) единицей измерения энтропии служит энтропия системы с десятью равновероятными состояниями, вычисленная с помощью десятичных логарифмов. Это десятичная единица энтропии – «дит».
Очевидно, что если в
системах с единичной энтропией принять закон равных вероятностей ![]() , то
, то
![]() и поскольку
и поскольку ![]() ,
то всегда N=a
,
то всегда N=a
На практике имеет место применение натурального логарифма с основанием е – в этом случае единица энтропии имеет название «нит».
Так как ![]() , то соотношения между единицами:
, то соотношения между единицами:
![]() бита
бита
![]() бита
бита
1дит=3,32бита, 1нит=1,51бита.
Рассмотрим ряд примеров по определению количества информации и энтропии.
Пример 1. Система имеет 64 элемента, один из которых неисправен. Вероятности того, что неисправен любой элемент, одинаковы. Определить количество информации I в сообщении о результате проверки одного элемента.
Каждый элемент есть источник с двумя состояниями: х1-исправен, х2-неисправен. Вероятности состояний показаны в таблице 1.6
|
|
|
|
|
|
|
|
Табл. 1.6
Количество частной информации I в сообщении, что проверяемый элемент исправен, равно
![]()
Количество частной информации I в сообщении, что проверяемый элемент неисправен, равно
![]()
Количество информации I(x) в сообщении о проверке одного элемента
![]() .
.
Пример 2. Вероятность выхода из строя некоторого прибора при включении равна Р0. После k-го включения прибор проверяют. Найти k из условия максимума информации, получаемой при проверке.
Вероятность
исправной работы после первого включения равна 1-р, после k-го
включения Рu=(1-p)k. Вероятность неисправного состояния после k-го
включения ![]() .
.
Максимум информации соответствует равновероятным состояниям, т.е.
![]() или
или
![]() , откуда
, откуда
![]() и
и 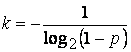 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.