Основы информатики и вычислительной техники: Учебно-практическое пособие, страница 17

В результате дискретизации во времени исходный непрерывный сигнал Х(t) представляется конечной последовательностью отдельных  значений Х(t_i), измеренных с шагом дискретизации ∆t=t_i-t_i-1. По значениям Х(t_i) можно восстановить исходный сигнал Х(t) с некоторой погрешностью. Функцию Х(t), полученную в результате восстановления (интерполяции) по значениям Х(t_i), называют воспроизводящей. При дискретизации возникает вопрос о точности преобразования, которая очевидно зависит от частоты отсчетов функции f_k=1/∆t_i, т.е. от выбранного шага дискретизации ∆t_i. С одной стороны, очевидно, что с уменьшением (увеличением) ∆t_i точность преобразования будет расти (уменьшаться) за счет увеличения (уменьшения) количества отсчетов. С другой стороны, очевидно, что нет смысла стремиться всегда брать отсчеты как можно чаще, независимо от вида сигнала Х(t), так как в случае медленно изменяющегося сигнала Х(t) два соседних значения Х(t_i) и  Х(t_i+1) могут быть настолько связаны (коррелированны)  между собой, что по одному из них Х(t_i) можно прогнозировать другое Х(t_i+1), т.е. никакой новой информации о сигнале при его последующем восстановлении по отсчетам это не дает. Проблема обеспечении точности дискретизации может быть сформулирована следующим образом: с каким максимальным интервалом необходимо брать отсчеты значений сигнала Х(t_i), чтобы не пропустить существенных его изменений или, другими словами, какое минимальное количество отсчетов необходимо брать для обеспечения заданной точности воспроизведения сигнала Х(t). От этого, в конечном счете, зависит количество информации, которую надо хранить и преобразовывать в вычислительном устройстве.

Возможны различные пути решения указанной проблемы.

В общем виде задача о представлении некоторого сигнала, являющегося непрерывной функцией времени, в виде конечного числа значений, взятых для дискретных значений времени, решена В.А. Котельниковым. В двух теоремах В.А. Котельников применительно к системе передачи сообщений по линии связи определил, как следует выбрать частоту дискретизации, обеспечивающую по полученным дискретным данным последующее воспроизведение исходного сигнала с заданной точностью.

Теорема 1. Любую функцию Х(t), имеющую спектр частот от 0 до f_m, можно представить суммой функции sinx/x, т.е. рядом:

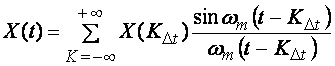        ,        (1.51)

где K – целое число,

      C– отсчеты мгновенных значений функции Х(t) с шагом дискретизации ∆t,

      ω_m = 2πf_m, f_m – максимальная частота в спектре частот сигнала Х(t), Гц

    ω_m – круговая частота.

Из этой теоремы может быть сделан и обратный вывод: любая функция, представленная рядом Котельникова (1.51), имеет спектр, состоящий из частот от 0 до f_m.

Теорема 2. Любая функция Х(t), содержащая частоты от 0 до f_m, полностью определяется дискретными значениями этой функции, следующими друг за другом с частотой 2f_m, т.е. через интервал 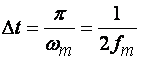 сек. Таким образом, передачу непрерывного сигнала Х(t) с ограниченным спектром частот, поступающего от какого-либо датчика, можно свести к передаче последовательности дискретных чисел – значений этого сигнала, взятых через интервал времени 1/2f_m; число этих значений равно 2f_m. Через полученные значения ординат, при обработке результатов измерений, можно провести единственным способом воспроизводящую непрерывную функцию. Поэтому, проще говоря, нет смысла брать отсчеты чаще, чем интервал 1/2f_m, так как никакой новой информации о функции при ее последующем восстановлении по отсчетам это не дает. Следует подчеркнуть, что сказанное справедливо только в том случае, если в получаемой информации действительно отсутствует частоты выше f_m.