Основы информатики и вычислительной техники: Учебно-практическое пособие, страница 11

Размерность корреляционной функции, как следует из (1.19) (1.20) равна квадрату размерности случайного сигнала. Практически это не всегда удобно (например, при сравнении корреляционных функций двух различных сигналов). Поэтому пользуются понятием нормированной (безразмерной) корреляционной функции , получаемой делением корреляционной функции на дисперсию:

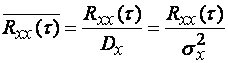                                       (1.23)

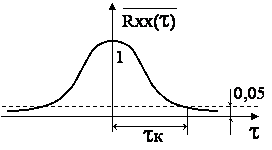Очевидно, что . При  ; при  . Примерный вид нормированной корреляционной функции показан на рис. 1.5.

Рис. 1.5. Нормированная корреляционная функция

Для случайных сигналов можно найти такой интервал времени , что при значения сигналов x(t) и x(t+τ) можно считать независимыми. Интервал времени , называемый интервалом корреляции, - это значение аргумента τ нормированной корреляционной функции, для которого (и всех больших значений) выполняется неравенство

где ε - любая, сколь угодно малая положительная величина. Практически значение τ_k определяют, задавая ε значение, равное 0,05.

Интервал корреляции используется при определении шага дискретизации по времени при аналого-цифровом преобразовании и передаче сигналов, при оценке энтропии сигнала, при прогнозировании сигналов, при анализе и синтезе автоматизированных информационных систем.

Эквивалентное число N практически независимых отсчетов, обработанных за время T наблюдения за сигналом (например, при оценке математических ожиданий, корреляционных функций и др.) определяется частным от деления времени наблюдения Т на интервал корреляции , т.е.

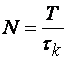                                                    (1.24)

Среди различных случайных процессов выделяют нормальный или гауссов процесс, полностью определяемый заданием математического ожидания и корреляционной функции. Такой процесс имеет место при действии большого числа независимых и непревалирующих факторов. Одномерная плотность вероятностей значений центрированного сигнала имеет вид

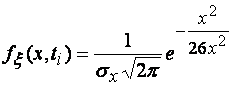
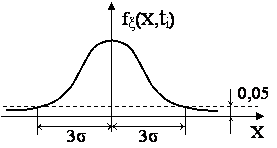Вероятность непопадания случайной величины в зону составляет менее 0,05 (рис. 1.6).

Рис. 1.6. Плотность вероятностей нормального процесса

Практически часто встречаются случаи, когда исследуется не один случайный сигнал x(t), а система, состоящая из двух случайных сигналов x(t) и y(t). Одномерная функция распределения такой системы случайных величин

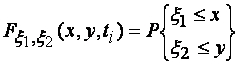                                     (1.25)

Одномерная плотность вероятностей

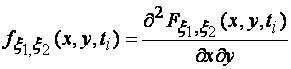                                    (1.26)

При этом в общем случае

(1.27)

где  - одномерная плотность вероятностей  при условии, что значение сигнала y(t) равно y(t_j);

          - одномерная плотность вероятностей  при условии, что значение сигнала х(t) равно х(t_j).