Определители. Формула Крамера решения системы линейных алгебраических уравнений. Элементы векторной алгебры и аналитической геометрии

Определители

Определение:            Прямоугольная таблица, состоящая из n-строк и m-столбцов называется матрицей размера . Если n = m, то матрица называется квадратной матрицей порядка m.

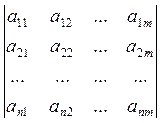
а₁₁ a₂₂ a₃₃ ... a_nm (если n=m) – главная диагональ 

a_1m a_2m-1 a_3m-1 – побочная диагональ

В каждой квадратной матрице ставится в соответствии число, называемое его определителем и обозначаемым  или detA.

detA = а₁₁ a₂₂ – a₁₂ a₂₁  для матрицы размером 2*2

detA = а₁₁ a₂₂ a₃₃ +а₁₃ a₂₁ a₃₂ +а₁₂ a₂₃ a₃₁ -а₁₃ a₂₂ a₃₁ -а₁₁ a₂₃ a₃₂ -а₁₂ a₂₁ a₃₃ для матрицы размером 3*3 (правило треугольников).

Определитель также называется детерминантом.

Свойства определителя:

1) Величина определителя меняет знак, если в матрице поменять местами 2 строки или 2 столбца.

 

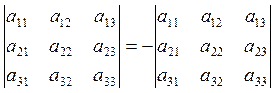
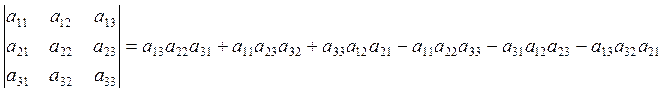
2) Матрица, получаемая из данной матрицы А заменой строк на столбцы, называется транспонированной матрицей А^Т к матрице А.       

        

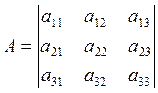
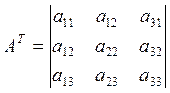
Определитель при транспонировании не меняется.

3) Вариант №1 – Определитель умножается на некоторое число к если элементы какого-либо столбца или строки умножаются на к.

Вариант №2 – Общий множитель в строке или столбце можно выносить за знак определителя.

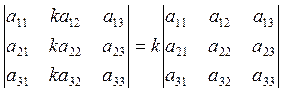
4) Если определитель имеет две одинаковых строки и столбца, то он равен 0.

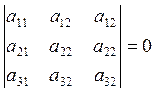
5) Если все элементы некоторой строки или некоторого столбца равны 0, то определитель равен 0.

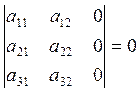
6) Если соответствующие элементы двух строк или столбцов пропорциональны, то определитель равен 0.

= 0

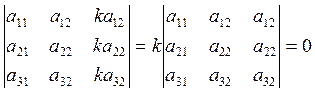
7) Если каждый элемент какого-либо столбца или строки равен сумме двух слагаемых, то определитель есть сумма двух определителей, из которых первых соответственно в столбце имеет первые слагаемые, второй – вторые, а элементы, стоящие в остальных столбцах у всех трех определителей одинаковы.

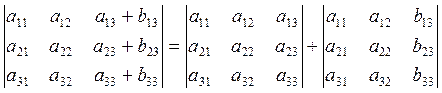
8) Если к  элементам некоторой строки или столбца прибавить элементы другого столбца или строки, умноженные на число, то величина определителя не изменится.

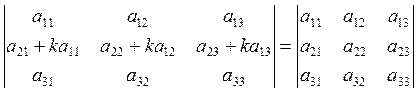
Минором M_ij некоторого элемента называется определитель, получающийся из данного вычеркиванием строки и столбца, на пересечении которых находится заданный элемент.

Пример:

        

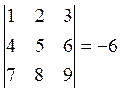
Алгебраическим дополнение A_ij элемента a_ij называется минор элемента, умноженного на

(-1)^i+j.

A₁₂  =  -6(-1)¹⁺²  =  6

9) Определитель равен сумме произведений элементов любой строки или столбца на их алгебраические дополнения.

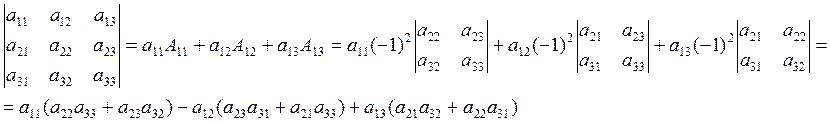 (Стандартная форма)

10) Сумма произведений элементов некоторой строки или столбца на алгебраические дополнения элементов  другой строки или столбца равны 0.

Формула Крамера решения системы линейных алгебраических уравнений.

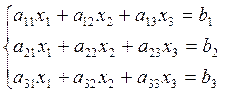       (1)

Если определитель не равен 0,то

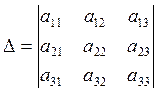
, где   - определитель системы.

(i=1,2,3) получается из определителя  путем замены i-столбца на столбец 1,2,3.

Пример:

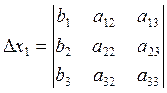
Доказательство: Умножим уравнения системы (1) на А₁₁, А₂₁, А₃₁ и всё это сложили.

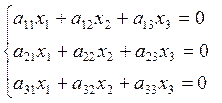 (2)

-  тривиальное решение

Если система имеет решение, при котором , то такое решение называется нетривиальным.

  

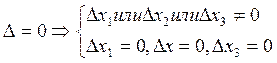
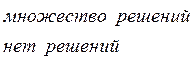
 - единственное решение

Теорема: Если определитель однородной системы не равен 0, то система имеет только тривиальное решение.

Если система имеет нетривиальное решение, то её определитель с необходимостью равен 0.

Элементы векторной алгебры и аналитической геометрии.

Элементы векторной алгебры.

Основные элементы.

Определение:            Величина, характеризуемая одним числовым значением, называется скаляром.

Определение:            Величина, характеризуемая числовым значением и направлением в пространстве, называется вектором.

Вектором  называется направленный отрезок с началом А и концом В.

Два вектора считаются равными если:

1)  равны числовые значения и характеризующие;

2)   их направление в пространстве совпадает.

Определение:             называется длиной отрезка, соединяющего концы вектора в пространстве.

Векторы, лежащие на одной прямой или на параллельных прямых, называются колониарные.

Если точки А и В совпадает, то вектор считается.

Длина равна 0, а направление не имеет смысла.

Вектор , длина которого (), называется единичным.

1)  Сложение векторов: Суммой двух векторов   и  называется вектор , выходящий из их общего начала, которое служит диагональю параллелограмма, сторонами которого является слагаемые вектора.

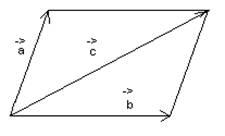
а) Переместительный закон

б) Сочетательный закон

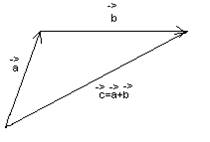
Правило сложения векторов: В конце вектора первого слагаемого строим второе слагаемое. Вектор, замыкающий эту ломаную, и есть сумма. Его начало совпадает с началом первого вектора, а конец с концом второго.

Вектор - называется противоположным вектору .

Разностью векторов  и  называется сумма вектора  с вектором -.

Определение:            Произведение вектора  на числоназывается вектор, имеющий длину  и направление при >0, совпадает с направлением вектора , при <0 противоположно направлению вектора , и при =0  вектор  =0.

Проекции векторов.