Определители. Формула Крамера решения системы линейных алгебраических уравнений. Элементы векторной алгебры и аналитической геометрии, страница 7

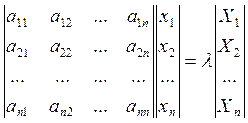
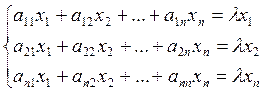
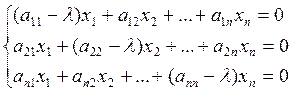      (1)

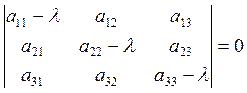    - характеристическое уравнение

Решая характеристическое уравнение, находим собственное значение , найденное  подставляется в систему (1) и из системы находятся координаты собственных векторов.

Пример:         Найти собственные значения и векторы , заданные в некотором базисе матрицы.

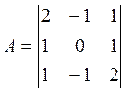
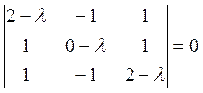
1)       

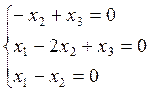
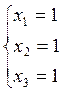
2)       

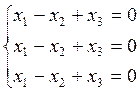
Теорема:        Если все собственные значения матрицы А линейного оператора  различны. То собственные векторы линейно-независимы.

Доказательство:        - собственные значения, а  - собственные векторы

Предположим противное – собственные векторы линейно-зависимы.

          

Применим к оператору :

 не может, так как  - собственный вектор.

Предположение не верно.

Следствие:    Если у  есть  собственных линейно-независимых векторов, где  - размерность пространства, то  в базисе из своих собственных векторов имеет вид:

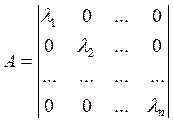
Определение:           Матрицу, доводимую к диагональному виду, называют матрицей простой структуры.

Вещественное Евклидово пространство.

Определение:           Вещественным линейным пространством называется Вещественное Евклидово пространство, если:

1)  Задан закон, по которому любым двум элементам x и y ставится в соответствие число называемое их скалярным произведением и обозначаемым ;

2)  Указанный закон подчинен 4-м аксиомам:

1.        

2.        

3.        

4.          при 

 при 

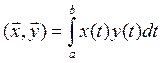
Линейное пространство  называется нормированным, если:

1)  есть правило, по которому  ставится в соответствие вещественное число называемое его нормой и обозначаемой  .

2)  указанное правило подчинено 3-м аксиомам:

1.          при

 при

2.        

3.        

В Евклидовом пространстве в качестве нормы можно использовать величину

В Евклидовом пространстве

Определение:            Углом между элементами x и y называют угол, косинус которого равен величине

Определение:            Элементы х и y называются ортогональными. Если их скалярное произведение равно 0:

Пример:        

n- элементов пространства   образуют ортонормированный базис, если   

   - верна, если и

Квадратичные формы.

Определение:                       Квадратичной формой переменных  называется однородный многочлен второй степени относительно этих переменных.

, где

Пример:        

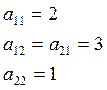
Определение:                       Матрица А называется матрицей квадратной формы в заданном базисе. Из условия следует, что , то матрица симметричная. Те

Теорема:        У любой симметричной матрицы А размером  существует n линейно-независимых попарно ортогональных и единичных собственных векторов. Чтобы привести квадратичную форму к каноническому виду необходимо привести ее матрицу к диагональному виду, так как матрица А симметрична, то в базисе из своих собственных векторов она будет иметь диагональный вид и, следовательно, в этом базисе иметь канонический вид.

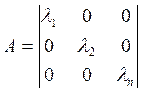
Пример:        

Привести квадратную форму к каноническому виду.

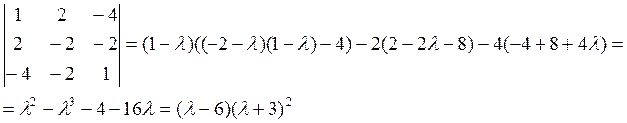
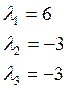
1)        Пусть

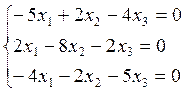
, то

2)        Пусть

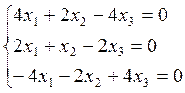
, то

, то

В базисе  А имеет диагональный вид:

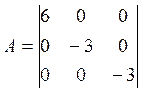
Приведение общего уравнения кривой второго порядка к каноническому виду.

1)  Записывают квадратичную форму соответствующую данной кривой

2)  Находят собственные значения и векторы, при чем собственные векторы нормируют.

3)  Вводят новые координаты, взяв в качестве нового базиса нормированные собственные векторы.

Т – матрица перехода

Т состоит из координат нового базиса по столбцам.

Введение нового базиса равносильно повороту системы на некоторый угол .

4)  Подставляют выражение старого через новый в слагаемых первого порядка.

5)  Выделяют полные квадраты и выполняют параллельный перенос координатных осей нового базиса, получая каноническое уравнение кривой.

1.           - эллипс действительный или мнимый.