Определители. Формула Крамера решения системы линейных алгебраических уравнений. Элементы векторной алгебры и аналитической геометрии, страница 5

Матрицу В называют обратной к матрице А, если АВ = ВА = Е.

Теорема:        У каждой квадратной невырожденной матрицы А порядка m существует одна обратная матрица , вычисляемая по формуле:

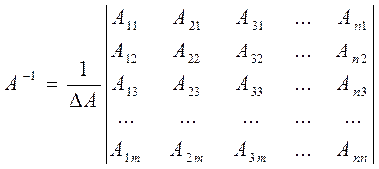
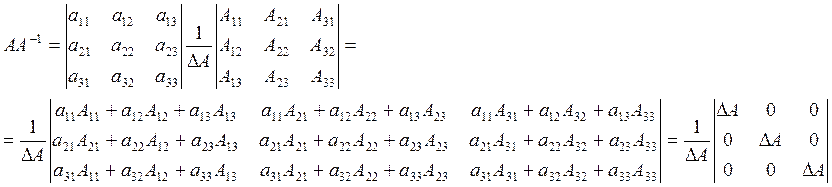
Пусть существует для  две обратных матрицы  и , тогда  и

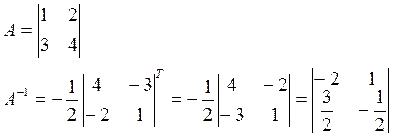
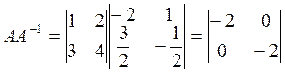
Матричный метод решения систем линейных алгебраических уравнений.

                   

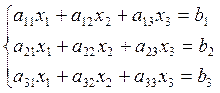
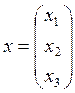
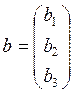
К недостаткам матричного способа относится очень большая трудоемкость, поэтому метод обычно применяют, когда надо решать одну и туже систему, но разными частями.

Ранг матицы

В матрице А размером  выбирают к строк и к столбцов.

Определение:            Минором к-го порядка матрицы А называется определитель к-го порядка, составленного из элементов матрицы А, распложенных на пересечении выбранных строк и столбцов.

 

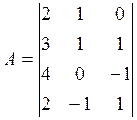
12 штук

18 штук

4 штук

Определение:            называют наибольший порядок, отличных от нуля миноров этой матрицы ()

К элементарным преобразованиям матрицы относятся умножение всех элементов некоторой строки а число , не равное 0, прибавление ко всем элементам строки соответствует элементов другой строки, умножение на некоторое число, перестановка строк, и все выше указанное для столбов.

Матрица, полученная одна из другой при помощи элементарных преобразований, называется эквивалентной.

Теорема:        эквивалентные матрицы имеют одни и тот же ранг.

Для вычисления ранга элементарными преобразованиями матрицу переводят в эквивалентную верхнетреугольную.

Ранг верхнетреугольной матрицы равен числу ненулевых элементов, стоящих на главной диагонали.

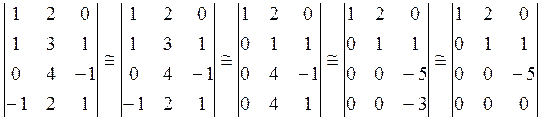
Метод Гаоса. Решение системы линейных уравнений. Метод последовательного исключения неизвестного.

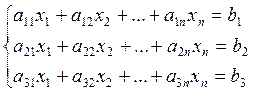
Расширенной матрицей системы  называется:

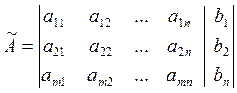
Приведение расширенной матрицы к верхнетреугольному виду с помощью элементарных преобразований.

Пример:

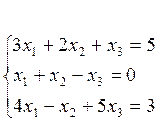
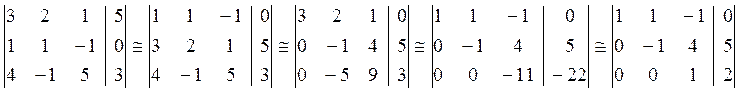
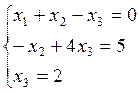
Условия совместимости системы. Критерий Кроникера-Капелли.

Теорема:                    Система линейных уравнений совместно тогда и только тогда, когда ранги матрицы системы и её расширенные матрицы совпадают.

Следствия:    1) Если система совместна, то при ранге, равном числу неизвестных система имеет единственное решение.

2) Если же ранг матрицы меньше числа неизвестных. То система имеет бесчисленное множество решений.

Линейное пространство.

Определение:            Линейным пространством называется множество двух элементов, если указан закон, по которому любым двум элементам x и y ставится в соответствии элемент z из L , называемый их суммой и обозначающий:

1)       

2)        Указан закон, по которому каждому числу  вещественному или комплексному и любому элементу x из L ставится в соответствии элемент z из L называется произведением элемента x на  и обозначается  и операция сложения и умножения на число удовлетворяющее следующим восьми аксиомам.

1)       

2)       

3)              

4)              

5)           

6)              

7)              

8)               

(пространство )

Функция задана на отрезке и непрерывна на нем.

  

- пространство функций, определенных на отрезке  и интегрируемых на нем.

Элементы линейного пространства называются векторами.

Определение:            Пространство  называется вещественным, если операция умножения определена для вещественных чисел и комплексным – для комплексных чисел.

Следствие: существует единственный нулевой вектор, каждый вектор имеет единственный пространственный вектор и  .

Линейная зависимость векторов.

Пусть  и - числа.

Определение:            Векторы  называются линейно-зависимыми, если существуют также коэффициенты , не равные одновременно 0, то линейная комбинация векторов () равна 0.

Определение:            Векторы называются линейно-независимыми, если линейная комбинация равна 0, то тогда и только тогда

Теорема:  линейно- зависимы тогда и только тогда, когда один из них есть линейная комбинация остальных.