Определители. Формула Крамера решения системы линейных алгебраических уравнений. Элементы векторной алгебры и аналитической геометрии, страница 2

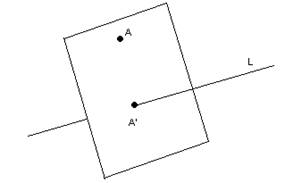
Определение:            Проекцией т.  на прямой L называется т. , в которой пересекаются прямая L с плоскостью, перпендикулярной к L и проходящей через А.

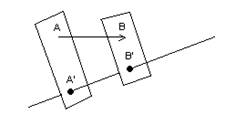
Направленная прямая называется осью.

Проекцией   на ось L называется вектор , где a’ и b’ – есть проекция точек a и b на L.

1)  Модуль проекции вектора на какую-либо ось L равен произведению данного вектора на косинус угла между осью и вектором.

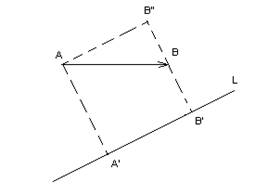
2)  Сумма векторов на любую ось равна сумме проекций слагаемых на эту ось.

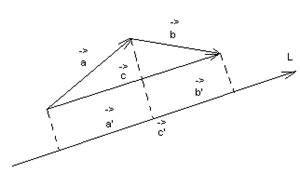
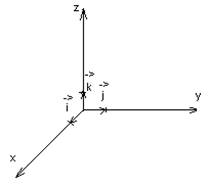
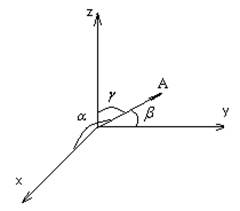
В прямоугольную систему координат входят три взаимоперпендикулярных оси, пересекающихся в т. 0.

Т. 0 называется началом координат и единичный отрезок, с помощью которого изменяются все остальные отрезки.

Пусть у нас есть некоторая т.А. Направленный отрезок ОА называется радиус-вектором т.А.

Определен вектор, который можно перемещать в пространстве.

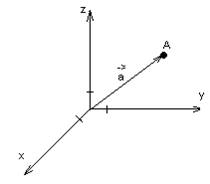
Числовые проекции вектора  0X, 0Y, 0Z являются X_a, Y_a, Z_a и называются координатами.

X – абсцисса, Y – ордината, Z – аппликата т. А

А 

А

 = (запись вектора в координатной форме)

Построить вектор , если  =

Два вектора называется равным, если равны их координаты:

 =

 =

      

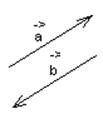
       колинеарность векторов

=

                     

 +  =

 =

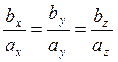
Векторы  называются ортами.

 = =

(векторная форма графика)

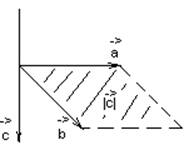
Всякий вектор можно разложить на 3 слагаемых, лежащих на осях координат. Эти слагаемые называются компонентами или составляющими данного вектора.

А

B

OA =

OB =

AB = OB - OA

AB =

Скалярное произведение векторов.

Скалярным произведением двух векторов называется число, равное произведению длин векторов на cos угла между ними.

Пример:

=6

=4

Из свойств проекции следует:

Скалярное произведение векторов  и , если произведение длины вектора  на числовую проекцию вектора  на вектор  или наоборот.

1) =

2) (+)=+

3) =()

4) =0, тогда и только тогда, когда  или один из векторов нулевой.

5)  = , так как cos 0 = 1

6) Если тело под действием силы F перемещается вдоль вектора , то работа силы равна скалярному произведению векторов  и .

A=

Пусть вектор  = =, а вектор  = =

=()()=

Пример:

а(2;-3;1)

b(0;2;-3)

Дж

Ответ: А=7Дж

=

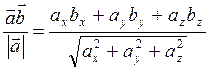
Определение:            Ортами вектора  называются векторы единичной длины, направленные так же как и вектор .

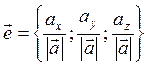
Доказательство: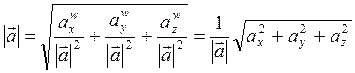

Направляющие косинусы

Направляющие косинусы – это косинусы углов, которые образуют вектор с осями координат.()

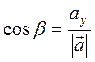
Направляющие косинусы  являются координатными ортами .

Доказательство:

Векторное произведение

Определение:            Тройка  называется правой тройкой, если с конца третьего вектора кратчайший поворот от первого вектора по второму вектору виден против часовой стрелки.

Определение:            Векторное произведение  и называется вектор , удовлетворяющий следующим 3 условиям ().

1)

2)

3)  - правая тройка

Геометрический смысл векторного произведения: модуль векторного произведения численно равен площади параллелограмма, построенного на векторах сомножителя.

Физический смысл векторного произведения: момент силы F относительно т. А равен векторному произведению вектора АВ на F(плечо на силу).

Свойства векторного произведения:

1)

2)

3)

4) , если  колинеарно  или один из сомножителей равен 0.

=

=

 =

 =

=()()=

  -    +   =

=

  =

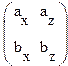
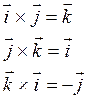
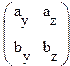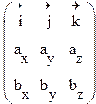
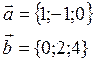
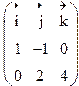
Пример: Найти площадь треугольника

А(-2;1;0)

В(1;4;-1)

С(0;3;2)

=

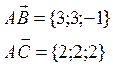
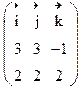Ответ:

Пример

= 

=

Ответ: S=21

Смешанное произведение векторов

Определение:            Смешанным произведением векторов  называется скаляр, равный скалярному произведением векторов  и .

Модуль смешанного произведения равен Vпар, построенного на данных векторах.

Пример:

А(2;1;-1)

В(0;3;1)

С(0;0;4)

D(-1;1;1)

V=

 

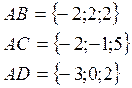
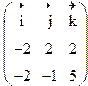
, если вектора   лежат в одной плоскости.

Определение:            3 вектора называются компланарными, если они параллельны одной плоскости. Необходимым и достаточным условием компланарности трех векторов является равенство 0 их смешенного произведения.