Определители. Формула Крамера решения системы линейных алгебраических уравнений. Элементы векторной алгебры и аналитической геометрии, страница 6

Доказательство: Необходимость – пусть вектора  линейно- зависимы

, то есть вектор  - есть линейная комбинация векторов .

Достаточно – дано, что один из векторов есть линейная комбинация остальных и доказать, что он – линейная зависимость остальных.

Если в линейном пространстве  существует  линейно– независимых векторов, а любые  линейно- независимы, то называется размерностью пространства мерного пространства или .

Линейная зависимость = колинеарность.

 неколинеарных вектора были линейно независимы.

 линейно- независимы = компланарность.  неколинеарных вектора линейно- независимы.

 линейно- независимых векторов. Любой вектор будет  зависим.

Определение:            Упорядоченная совокупность векторов линейного пространства  называется базисом этого пространства, если эти векторы линейно- независимы и  может быть представлен как линейная комбинация этих векторов.

      (1)

Равенство (1) называется разложением векторов по базису , а числа  координатами вектора  в этом базисе.

Теорема: Любой вектор  пространства  можно разложить по базису этого пространства и при том единственным образом.

Признаки линейной зависимости вектора

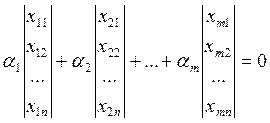
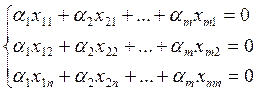
 система имеет множество решений, в том числе и нетривиальное решение, а это означает линейную зависимость векторов. Если , то вектора линейно - независимы.

Пример:

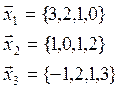
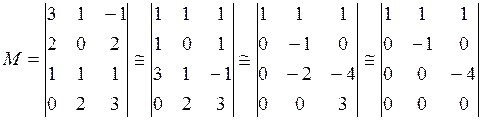
Пример:

Даны координаты  в старом базисе. Найти координаты  в новом базисе.

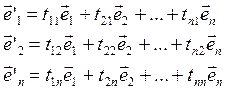
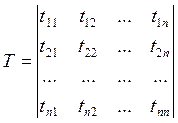
Матрица Т называется матрицей перехода.

 следует из независимости .

Пусть вектор

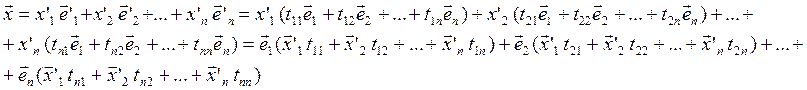
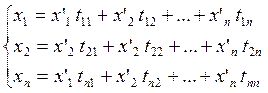
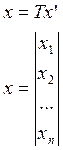
Пример: Вектор  в стандартном базисе пространства  

Найти координаты  в базисе и , если  и

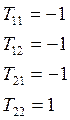
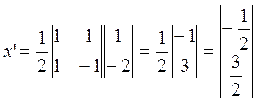
Линейный оператор

 и  - два линейных пространства

 называется отображение сопоставляющее каждому   некоторого

Вектор  называется образом вектора . А вектор  - прообразом .

Определение:            Оператор  называется линейным, если:

1.        

2.        

Пусть - базис в

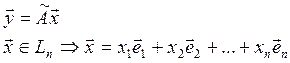
- координаты вектора  в , тогда в силу единства разложения вектора по базису получаем:

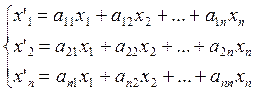
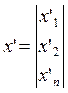, где  и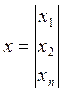

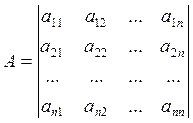
Каждому линейному оператору соответствует матрица А, составленная из элементов , называется матрицей линейного оператора, каждый столбец которой образован коэффициентами разложения вектора  по базису.

Определение:            Матрица А называется матрицей преобразования, если  только при, то оператор называют невырожденным.

Если существует  такой, что , то такой оператор называется вырожденным.

Для того чтобы оператор  был невырожденным необходимо и достаточно, чтобы определитель матрицы оператора  был отличен от 0.

Пример: Линейных оператор  действует на плоскость XOY и является оператором растяжения вдоль оси OY в R раз. Составить матрицу оператора в стандартном базисе.

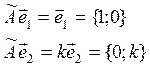
Действия с линейными операторами.

Линейный оператор матрица линейного оператора.

1.  Сложение операторов.

Суммой двух линейных операторов  и  называется оператор , такой что . Матрица оператора

2.  Произведение линейного оператора  на называется оператором , такой что . Матрица оператора  равна произведению числа  на матрицу оператора .

3.  Произведение линейных операторов  и  называется оператор , такой что . Матрица С равна произведению А и В.

Замечания:

1.          и  описывают действия одного и того же оператора, но в разных базисах.

2.        

Собственные значения и собственные векторы линейного оператора.

Определение:           Ненулевой вектор  называется собственным вектором , если справедливо равенство .

Определение:           Скаляр  называется собственным значением линейного оператора, соответствующее собственному вектору .

Теорема:        Если  - некоторый собственный вектор (), то вектор , где  - отличное от нуля, также является собственным вектором, отвечающим тому же собственному значению.

Доказательство:      

Пусть в пространстве  существует базис , тогда  и вектор .