Доказательство: Обратная утверждение теоремы неверно. Условие теоремы необходимо, но достаточно.
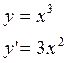
![]() т. 0 – не точка экстремума.
т. 0 – не точка экстремума.
Пусть функция ![]() непрерывна на интервале, содержащем т.
непрерывна на интервале, содержащем т. ![]() , и дифференцируема на нем может быть,
кроме т.
, и дифференцируема на нем может быть,
кроме т. ![]() . Если при переходе слева направо через
. Если при переходе слева направо через ![]() производная меняет знак с плюса на
минус, то в этой точке максимум, если наоборот, то минимум.
производная меняет знак с плюса на
минус, то в этой точке максимум, если наоборот, то минимум.
Пусть т. ![]() , такая что
, такая что ![]() , а
, а ![]() , то
, то ![]() по
теореме Лагранжа =
по
теореме Лагранжа = ![]() .
.
1) ![]()
![]()
![]()
2) ![]()
![]()
![]()
Второе достаточное условие экстремума.
Пусть ![]() - критическая точка функции
- критическая точка функции ![]() , тогда, если
, тогда, если ![]() то
т.
то
т. ![]() максимум, а если
максимум, а если ![]() то т.
то т. ![]() минимум.
минимум.
Если ![]() то эта точка как может быть экстремумом,
так и не может.
то эта точка как может быть экстремумом,
так и не может.
Схема исследования дифференциальной функции с помощью первой производной.
1) Найти производную.
2) Найти критические точки функции.
3) Проверить достаточное условие экстремума в критических точках.
4) Найти экстремальное значение функции.
Пример: ![]()
1) ![]()
2) ![]()
![]()
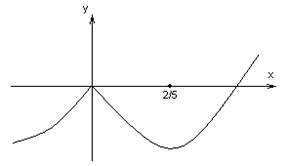
3)
![]()
4) ![]()
![]()
|
|
|
0 |
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
0 |
|
|
|
|
|
|
Наибольшее и наименьшее значения.
Функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]()
![]() на нем
достигает своего наименьшего и наибольшего значений. Наименьшие и наибольшие
значения также достигаются на концах отрезка или в критических точках.
на нем
достигает своего наименьшего и наибольшего значений. Наименьшие и наибольшие
значения также достигаются на концах отрезка или в критических точках.
Схема исследования.
1)
Находят производную ![]()
2) Находят критические точки функции
3)
Считают ![]() и значение функции в
критических точках, из которых выбирают наименьшее и наибольшее.
и значение функции в
критических точках, из которых выбирают наименьшее и наибольшее.
Пример: ![]() при
при ![]()
1) ![]()
2) ![]()
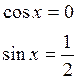
![]()
![]()
![]()
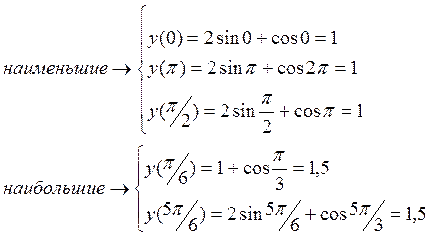
Выпуклость и вогнутость кривой.
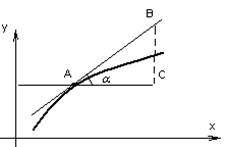
Кривая выпукла
на интервале ![]() , если все точки кривой лежат ниже любой
ее касательной на этом интервале.
, если все точки кривой лежат ниже любой
ее касательной на этом интервале.
![]()

Кривая называется вогнутой, если все точки кривой лежат выше касательных на этой кривой.
![]()

Теорема:
1)
Если во всех точках интервала ![]() вторая производная
функции
вторая производная
функции ![]() положительная, то кривая на этом
интервале вогнутая.
положительная, то кривая на этом
интервале вогнутая.
2)
Если во всех точках интервала ![]() вторая производная
функции
вторая производная
функции ![]() отрицательная, то кривая на этом
интервале выпуклая.
отрицательная, то кривая на этом
интервале выпуклая.
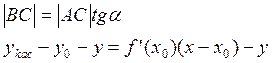
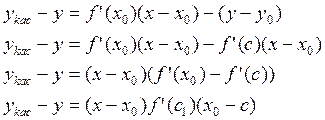
1) ![]()
![]()
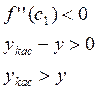
2) ![]()
![]()
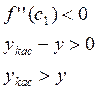
![]() Функция
Функция ![]() выпукла.
выпукла.
Определение: Точки кривой, отделяющие выпуклость и вогнутость называются точками перегиба.

Теорема: Пусть
вторая производная функции ![]() в т.
в т. ![]() = 0 или не существует, если при переходе
функции через
= 0 или не существует, если при переходе
функции через ![]() слева направо знак второй
производной меняется на противоположный, то т.
слева направо знак второй
производной меняется на противоположный, то т. ![]() является
точкой перегиба кривой.
является
точкой перегиба кривой.
Асимптоты
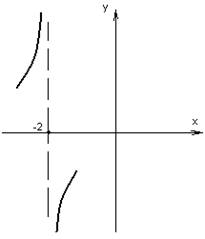
Определение: Прямая
![]() называется вертикальной асимптотой
кривой, если хотя бы один из пределов бесконечен.
называется вертикальной асимптотой
кривой, если хотя бы один из пределов бесконечен.
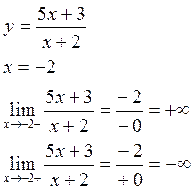
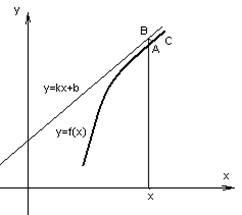
Наклонная асимптота.
![]()
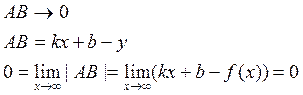
![]()
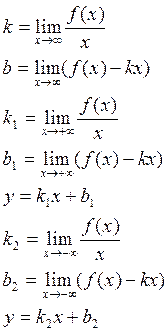
У периодических функций асимптот нет.
Пример: ![]()
Вертикальные асимптоты:
![]()
![]()
![]()
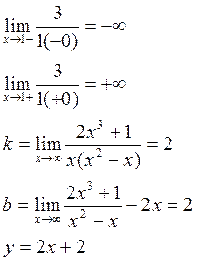
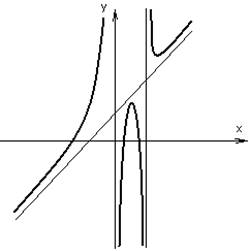
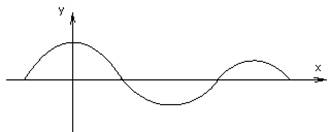
Пример: ![]()
Вертикальных асимптот нет.
![]()
При ![]() наклонных асимптот нет.
наклонных асимптот нет.
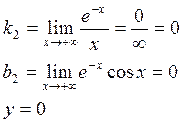
Полное исследование функции.
1) Область определения
2) Четность, нечетность
3) Периодичность
4) Точки пересечения с осями (если возможно)
5) Точки разрыва
6) Асимптоты
7) Точки экстремума, интервалы возрастания и убывания
8) Выпуклость и вогнутость.
Пример: ![]()
1) ![]()
2) Функция общего вида.
3) Непериодическая
4) Точка
пересечения с осями - ![]()
5) ![]() - точка разрыва второго рода.
- точка разрыва второго рода.
![]()
![]()
6) ![]() - вертикальная асимптота
- вертикальная асимптота
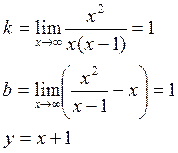
7) ![]()
![]()
|
|
|
0 |
|
2 |
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
0 |
|
4 |
|
|
|
|
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.